pas facile cette figure !
Question équation non linéaire (en dimension 1) c'est possible
http://asymptote.sourceforge.net/doc/Ma ... ctions-631
la méthode de Newton-Raphson (donc connaître
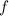 et
et 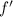 ) est implémentée.
) est implémentée.O.G.
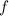 et
et 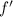 ) est implémentée.
) est implémentée.projetmbc a écrit :Très parlant ton exemple....Il est où...
Code : Tout sélectionner
unitsize(4cm,8cm);
import graph;
real t;
path Cf,Cg,Ch;
real xd=1/3+0.000001, xa=100,
prec=.0001,
diff_aires;
int np=10000;
real a,b,c;
for(int i=-27; i<10; ++i){
write(i);
diff_aires=2*prec;
t=1+i/100;
real f(real x){return 8*t/(3*x-1)-3/x^2;}
Cf=graph(f,xd,xa,n=np,Spline);
if(t<1){
Cg=subpath(Cf,dirtime(Cf,(1,0)),reltime(Cf,1));
Cg=subpath(Cg,0,maxtimes(Cg)[1]);
a=min(Cg).y;
b=max(Cg).y;
while(abs(diff_aires)>prec)
{
c=(a+b)/2;
real[] zi=times(Cf,(0,c));
if(zi.length!=3) {
write("attention");
break;
}
real g(real x){return f(x)-c;}
diff_aires=simpson (g, point(Cf,zi[0]).x,point(Cf,zi[2]).x);
if(diff_aires<0) b=c; else a=c;
}
real h(real x){return c;}
path Ch=graph(h,xd,xa,n=2);
real[] zi=times(Cf,(0,c));
if(zi.length==3) Cf=firstcut(Cf,Ch).before--lastcut(Cf,Ch).after;
write(zi);
}
draw(Cf);
}
xlimits(-.5,4.5,Crop);
ylimits(-.2,1.5,Crop);
xaxis(Label("$x$",position=EndPoint, align=SE),
xmin=0, xmax=4.6,
Ticks(scale(.7)*Label(),
NoZero,
Step=.5,step=.1,
Size=2mm, size=1mm,
pTick=black,ptick=gray),
Arrow);
yaxis(Label("$y$",position=EndPoint, align=NE),
ymin=-.1,ymax=1.55,
Ticks(scale(.7)*Label(),
NoZero,
Step=0.5,step=.1,
Size=2mm, size=1mm,
pTick=black,ptick=gray),
Arrow);
write("patienter encore un peu...");
GM a écrit :Un essai (avec un problème)... que je n'ai pas le temps d'améliorer avant le weekend prochain.
Le problème : je crois qu'il se voit... et je n'ai pas encore compris pourquoi.
Les améliorations : tracer la courbe de coexistence... puis après tracer le faisceau de courbes dans l'espace.
Code : Tout sélectionner
> palier:=proc(temp) option remember; local vL,vV,pL,eq1,eq2;
> eq1:=subs(v_V=vV,v_L=vL,t=temp,palier_pression);
> eq2:=subs(v_V=vV,v_L=vL,t=temp,maxwell);
> fsolve({eq1,eq2},{vL,vV},{vL=0..1,vV=1..infinity});
> assign(%);
> [vL,vV,f(vL,temp)];
> end;
Code : Tout sélectionner
Cg=subpath(Cf,dirtime(Cf,(1,0)),reltime(Cf,1));
Cg=subpath(Cg,0,maxtimes(Cg)[1]);
cjorssen a écrit :J'ai commencé à regarder et je ne comprends pas bien ce que font ces lignesCode : Tout sélectionner
Cg=subpath(Cf,dirtime(Cf,(1,0)),reltime(Cf,1));
Cg=subpath(Cg,0,maxtimes(Cg)[1]);
Tu cherches une tangente horizontale avec dirtime(Cf,(1,0)) ?
Code : Tout sélectionner
unitsize(4cm,8cm);
import graph;
// t est la température réduite
real t;
// C_isotherme_VdW : isotherme de Van der Walls (conduisant pour t<1
// à des propriétés non physiques)
path C_isotherme_VdW;
// C_isotherme_Andrews : isotherme de Van der Walls corrigées
// (palier de liquéfaction)
path C_isotherme_Andrews;
// Cg et C_palier sont des courbes auxiliaires nécessaires au calcul
path Cg,C_palier;
// vmin et vmax sont les bornes du volume réduit utilisées pour la
// détermination du palier de liquéfaction (ne correspond pas forcément
// aux bornes de l'affichage définitif)
// On prend vmin très légèrement supérieur à 1/3 car sinon problème de
// définition de la pression réduite p (voir infra)
real vmin=1/3+0.000001;
real vmax=30;
// precision est la précision du calcul d'aire (Maxwell)
real precision=.0001;
// Variable auxiliaire pour le calcul d'aire
real diff_aires;
// nb_points est le nombre de points servant à obtenir C_isotherme_VdW
int nb_points=1000;
// Variables auxiliaires
real a,b,c;
// Boucle sur différentes valeurs de la température réduite
for(int i=-27; i<10; ++i){
t=1+i/100;
write(t);
// Équation de Van der Waals en coordonnées réduites
real p(real v){return 8*t/(3*v-1)-3/v^2;}
// La courbe représentant l'isotherme de Van der Waals est calculée
C_isotherme_VdW=graph(p,vmin,vmax,n=nb_points,Spline);
if(t>=1){
// Si la température critique est supérieure à 1, le fluide de Van der
// Waals est supercritique. Il ne subit pas de changement d'état.
// L'isotherme d'Andrews est identique à l'isotherme de Van der Waals.
C_isotherme_Andrews=C_isotherme_VdW;}
else{
// Sinon, il faut déterminer la position du palier de liquéfaction.
// Ici, on utilise la construction de Maxwell : voir par exemple
// www.lerepairedessciences.fr/sciences/agregation_fichiers/thermo/maxw.pdf
//
// Soit v1 le volume réduit corespondant au minimum
// (tangente horizontale) de l'isotherme de Van der Waals.
// Cg est l'isotherme de Van der Waals pour v > v1.
Cg=subpath(C_isotherme_VdW,
dirtime(C_isotherme_VdW,(1,0)),
reltime(C_isotherme_VdW,1));
// Soit v2 le volume réduit correspondant au maximum de l'isotherme de
// Van der Waals. Cg est l'isotherme de Van der Waals pour v1 < v < v2.
Cg=subpath(Cg,0,maxtimes(Cg)[1]);
// a est la pression réduite pour le volume v1 (le minimum de p)
a=min(Cg).y;
// b est la pression réduite pour le volume v2 (la maximum de p)
b=max(Cg).y;
// On initialise diff_aires à une valeur supérieure pour rentrer dans
// la boucle while
diff_aires=2*precision;
while(abs(diff_aires)>precision)
{
// On amorce une boucle pour procéder par dichotomie afin
// de trouver la pression réduite du palier de liquéfaction
// donnant des aires égales compte tenu de la précision
// demandée.
c=(a+b)/2;
// v_palier_inter_isotherme_VdW est un tableau donnant généralement
// 3 valeurs de v correspondant à la valeur de la pression d'essai
// du palier stockée dans c
real[] v_palier_inter_isotherme_VdW=times(C_isotherme_VdW,(0,c));
if(v_palier_inter_isotherme_VdW.length!=3) {
// Problème...
write("attention");
break;
}
// Pour calculer l'aire de Maxwell, il faut recentrer les courbes
// sur l'axe des abscisses. On retranche dans à la pression de Van
// der Waals p(v) la pression d'essai du palier c.
real g(real v){return p(v)-c;}
// Méthode de simpson pour le calcul d'intégrale
diff_aires=simpson(g,
point(C_isotherme_VdW,
v_palier_inter_isotherme_VdW[0]).x,
point(C_isotherme_VdW,
v_palier_inter_isotherme_VdW[2]).x);
// Dichotomie
if(diff_aires<0) b=c; else a=c;
}
// Construction du palier (la pression réduite de liquéfaction vaut c)
real h(real v){return c;}
// Deux points suffisent pour construire une droite
path C_palier=graph(h,vmin,vmax,n=2);
real[] v_palier_inter_isotherme_VdW=times(C_isotherme_VdW,(0,c));
if(v_palier_inter_isotherme_VdW.length==3){
C_isotherme_Andrews=firstcut(C_isotherme_VdW,C_palier).before
-- lastcut(C_isotherme_VdW,C_palier).after;}
write(v_palier_inter_isotherme_VdW);
}
draw(C_isotherme_Andrews);
}
xlimits(-.5,4.5,Crop);
ylimits(-.2,1.5,Crop);
xaxis(Label("$x$",position=EndPoint, align=SE),
xmin=0, xmax=4.6,
Ticks(scale(.7)*Label(),
NoZero,
Step=.5,step=.1,
Size=2mm, size=1mm,
pTick=black,ptick=gray),
Arrow);
yaxis(Label("$y$",position=EndPoint, align=NE),
ymin=-.1,ymax=1.55,
Ticks(scale(.7)*Label(),
NoZero,
Step=0.5,step=.1,
Size=2mm, size=1mm,
pTick=black,ptick=gray),
Arrow);
write("patienter encore un peu...");
GM a écrit :cjorssen a écrit :J'ai commencé à regarder et je ne comprends pas bien ce que font ces lignesCode : Tout sélectionner
Cg=subpath(Cf,dirtime(Cf,(1,0)),reltime(Cf,1));
Cg=subpath(Cg,0,maxtimes(Cg)[1]);
Tu cherches une tangente horizontale avec dirtime(Cf,(1,0)) ?
Exactement.
cjorssen a écrit :J'ai repris ton code que j'ai commenté et j'ai un peu changé les notations pour les variables afin que cela soit plus "physique". J'espère que tu ne m'en voudras pas
GM a écrit :Le problème : je crois qu'il se voit... et je n'ai pas encore compris pourquoi.
Code : Tout sélectionner
a=min(Cg).yCode : Tout sélectionner
a=max(min(Cg).y,.02);