
|
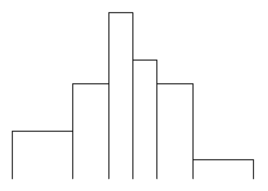
import stats; import graph; size(7cm,5cm,false); // Tableau des valeurs définissant les classes real[] tabxi={0,5,8,10,12,15,20}; // Tableau des effectifs (ou fréquences) des classes real[] tabni={5,6,7,5,6,2}; // Calcul des hauteurs real[] tabhi; for(int i=0; i < tabni.length; ++i) tabhi[i]=tabni[i]/(tabxi[i+1]-tabxi[i]); // Tracé de l'histogramme histogram(tabxi,tabhi,low=0,bars=true); shipout(bbox(3mm,white)); |

|
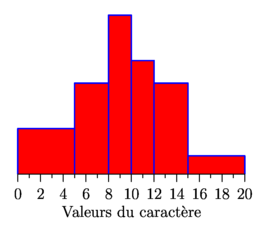
import stats; import graph; size(7cm,6cm,false); // Tableau des valeurs définissant les classes real[] tabxi={0,5,8,10,12,15,20}; // Tableau des effectifs (ou fréquences) des classes real[] tabni={5,6,7,5,6,2}; // Calcul des hauteurs real[] tabhi; for(int i=0; i < tabni.length; ++i) tabhi[i]=tabni[i]/(tabxi[i+1]-tabxi[i]); // Tracé de l'histogramme histogram(tabxi,tabhi,low=0,bars=true,red,1bp+blue); xaxis("Valeurs du caract\`ere",Bottom, RightTicks(Step=2,step=1),above=true); shipout(bbox(3mm,white)); |

|
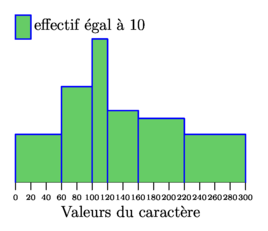
import stats; import graph; size(7cm,6cm,false); // Tableau des valeurs définissant les classes real[] tabxi={0,60,100,120,160,220,300}; // Tableau des effectifs (ou fréquences) des classes real[] tabni={60,80,60,60,80,80}; // L'unité d'aire (dont la largeur sera celle de la classe // de plus petite amplitude) indiquera un effectif égal à... real uniteaire=10; string libelleunite="effectif \'egal \`a 10"; // Le style des rectangles pen p1=.8lightgreen,p2=1bp+blue; // Libellé du caractère étudié string libellecaractere="Valeurs du caract\`ere"; // Paramètres de l'axe des abscisses real minaxe=0; real maxaxe=300; real uniteaxe=20; /////////////////////////////////////////////////////////////// /// Ce qui suit n'est a priori pas à changer et pourrait être /// ajouté un de ces jours à une extension perso stats_gm.asy /// pour être remplacé par : /// histogram(tabxi,tabhi,low=0,bars=true,p1,p2, /// uniteaire,libelleunite,libellecaractere); /////////////////////////////////////////////////////////////// // Une variable utile pour déterminer la plus petite amplitude : real largeurunite=abs(tabxi[1]-tabxi[0]); // ... et une autre pour le numéro de classe correspondant : int iclasse=0; // Calcul des hauteurs (et de la plus petite amplitude de classe) : real[] tabhi; for(int i=0; i < tabni.length; ++i){ tabhi[i]=tabni[i]/(tabxi[i+1]-tabxi[i]); if (largeurunite>abs(tabxi[i+1]-tabxi[i])) { largeurunite=abs(tabxi[i+1]-tabxi[i]); iclasse=i; } } // Hauteur du rectangle le plus haut pour placer l'unité au dessus. real hauteurmaxi=max(tabhi); // Calcul de la hauteur à donner au rectangle unité d'aire real hauteurunite=(uniteaire/tabni[iclasse])*tabhi[iclasse]; // Tracé de l'histogramme histogram(tabxi,tabhi,low=0,bars=true,p1,p2); // Tracé de l'unité d'aire et son étiquette filldraw(box((0,hauteurmaxi),(largeurunite,hauteurmaxi+hauteurunite)),p1,p2); label(libelleunite,(largeurunite,hauteurmaxi+hauteurunite),SE); // Ajout de l'axe gradué xaxis(libellecaractere, Bottom, minaxe,maxaxe, RightTicks(Label(currentpen+fontsize(6)), Step=uniteaxe),above=false); /////////////////////////////////////////////////////////////// shipout(bbox(3mm,white)); |

|
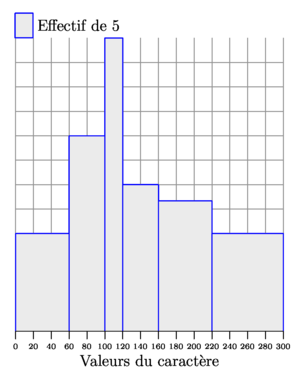
// gm.asy est une extension personnelle (avec des définitions en phase de test) // téléchargeable ici : gm.asy import gm; size(8cm,10cm,false); // Tableau des valeurs définissant les classes real[] tabxi={0,60,100,120,160,220,300}; // Tableau des effectifs (ou fréquences) des classes real[] tabni={60,80,60,60,80,80}; histogramme(tabxi,tabni, uniteaxe=20, // (maxaxe-minaxe)/4 par défaut // libellecaractere="Valeurs du caract\`ere", libelleunite="Effectif de ", // frequence=false, // false par défaut // pourcent=false // false par défaut uniteaire=5 // sum(tabni)/100 par défaut ); // ATTENTION, cette fonction n'est pas encore // au point pour passer facilement des effectifs // aux fréquences ou le contraire. shipout(bbox(3mm,white)); |

|
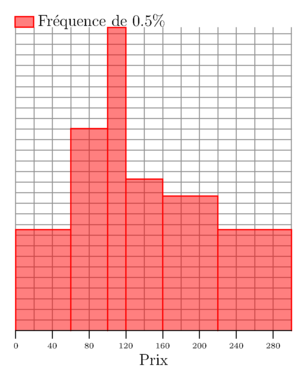
// gm.asy est une extension personnelle (avec des définitions en phase de test) // téléchargeable ici : gm.asy import gm; size(8cm,10cm,false); // Tableau des valeurs définissant les classes real[] tabxi={0,60,100,120,160,220,300}; // Tableau des effectifs (ou fréquences) des classes real[] tabni={60,80,60,60,80,80}; histogramme(tabxi,tabni, p1=.8bp+red+opacity(.5), p2=.8bp+red, uniteaxe=40, // (maxaxe-minaxe)/4 par défaut libellecaractere="Prix", libelleunite="Fr\'equence de ", frequence=true, // false par défaut pourcent=true, // false par défaut uniteaire=0.5 // 1% par défaut ); // ATTENTION, cette fonction n'est pas encore // au point pour passer facilement des effectifs // aux fréquences ou le contraire. shipout(bbox(3mm,white)); |

|
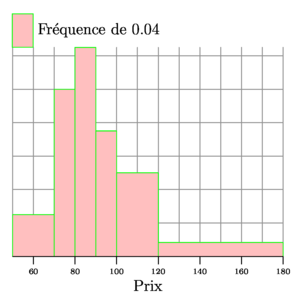
// gm.asy est une extension personnelle (avec des définitions en phase de test) // téléchargeable ici : gm.asy import gm; size(8cm,8cm,false); // Tableau des valeurs définissant les classes real[] tabxi={50,70,80,90,100,120,180}; // Tableau des effectifs (ou fréquences) des classes real[] tabni={.1,.2,.25,.15,.2,.1}; histogramme(tabxi,tabni, p1=palered, p2=.5bp+green, uniteaxe=20, // (maxaxe-minaxe)/4 par défaut libellecaractere="Prix", libelleunite="Fr\'equence de ", frequence=true, // false par défaut pourcent=false, // false par défaut uniteaire=4 // 1% par défaut ); shipout(bbox(3mm,white)); |

|
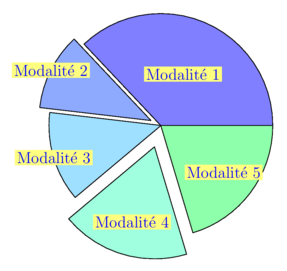
size(7.5cm,0); // Tableau des modalités string[] tabmod={"Modalit\'e 1","Modalit\'e 2","Modalit\'e 3", "Modalit\'e 4","Modalit\'e 5"}; // Tableau des effectifs (ou fréquences) real[] tabeff={20,6,7,10,11}; // Tableau des décalages éventuels des secteurs real[] tabdecsec={0,.1,0,.2,0}; // Tableau des décalages éventuels des labels real[] tabdeclab={0,.5,.5,.2,.2}; // Les deux couleurs utilisées pour composer // les couleurs des secteurs pen color1=green,color2=blue; // Le stylo pour les labels pen p3=blue,p4=yellow+white; /////////////////////////////////////////////////////////////// /// Ce qui suit n'est a priori pas à changer et pourrait être /// ajouté un de ces jours à une extension perso stats_gm.asy /// pour être remplacé par : /// diacirculaire(tabmod,tabeff,tabdec,color1,color2); /////////////////////////////////////////////////////////////// real[] tabangle,tabanglecumule,tabanglelabel; tabanglecumule[0]=0; int n=tabeff.length; for(int i=0; i<n; ++i) { tabangle[i]=tabeff[i]*360/sum(tabeff); tabanglecumule[i+1]=tabanglecumule[i]+tabangle[i]; tabanglelabel[i]=tabanglecumule[i]+tabangle[i]/2; path secteur=(0,0)--arc((0,0),1,tabanglecumule[i],tabanglecumule[i+1])--cycle; transform t1=shift(tabdecsec[i]*dir(tabanglelabel[i])), t2=shift((.5+tabdecsec[i]+tabdeclab[i])*dir(tabanglelabel[i])); filldraw(t1*secteur,i/n*color1+(1-i/n)*color2+white); label(tabmod[i],t2*(0,0),p3,Fill(p4)); } shipout(bbox(3mm,white)); |

|
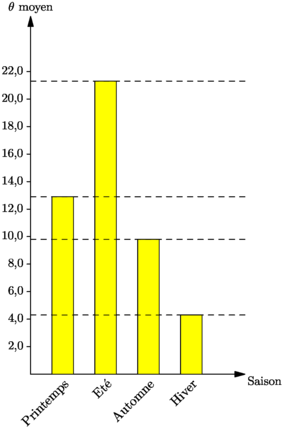
size(7.5cm,0); void bargraph(real X, real Y, real ymin, real ymax, real ystep, real tickwidth, string yformat, Label LX, Label LY, Label[] LLX, real[] height, pen p=nullpen){ draw((0,0)--(0,Y),EndArrow); draw((0,0)--(X,0),EndArrow); label(LX,(X,0),plain.SE,fontsize(9)); label(LY,(0,Y),plain.N,fontsize(9)); real yscale=Y/(ymax+ystep); for(real y=ymin; y<ymax; y+=ystep) { draw((-tickwidth,yscale*y)--(0,yscale*y)); label(format(yformat,y),(-tickwidth,yscale*y),plain.W,fontsize(9)); } int n=LLX.length; real xscale=X/(2*n+2); for(int i=0;i<n;++i) { real x=xscale*(2*i+1); path P=(x,0)--(x,height[i]*yscale)--(x+xscale,height[i]*yscale)--(x+xscale,0)--cycle; fill(P,p); draw(P); label(LLX[i],(x+xscale/2),plain.S,fontsize(10)); } for(int i=0;i<n;++i) draw((0,height[i]*yscale)--(X,height[i]*yscale),dashed); } string yf="%#.1f"; Label[] LX={"Printemps","Et\'e","Automne","Hiver"}; for(int i=0;i<LX.length;++i) LX[i]=rotate(45)*LX[i]; real[] H={12.9,21.3,9.8,4.3}; bargraph(X=60,Y=100, ymin=2,ymax=24,ystep=2, tickwidth=1, yf, "Saison","$\theta$ moyen", LX,H, yellow); |

|
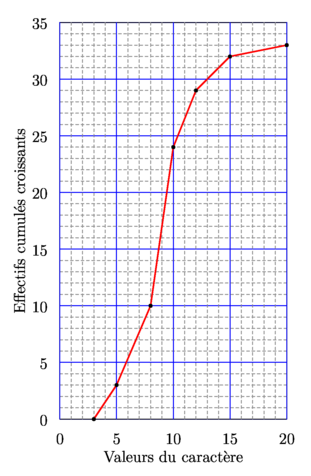
import graph_pi; real xmin=0, xmax=20, ymin=0, ymax=35; graphicrules(xunit=.3cm, yunit=.3cm, xmin=xmin, xmax=xmax, ymin=ymin, ymax=ymax, crop=Crop ); xaxis("Valeurs du caract\`ere",BottomTop, Ticks(Step=5,step=1, pTick=blue, ptick=linetype("4 4")+grey, extend=true)); yaxis("Effectifs cumul\'es croissants",LeftRight, Ticks(Step=5,step=1, pTick=blue, ptick=linetype("4 4")+grey, extend=true)); // Tableau des valeurs définissant les classes real[] tabxi={3,5,8,10,12,15,20}; // Tableau des effectifs des classes int[] tabni={3,7,14,5,3,1}; // Calcul des effectifs cumulés int[] tabecc; tabecc[0]=0; for(int i=1; i <= tabni.length; ++i) tabecc[i]=tabni[i-1]+tabecc[i-1]; // Tracé du polygone des effectifs cumulés croissants path polygone=graph(tabxi,tabecc); draw(polygone,1bp+red); dot(polygone); shipout(bbox(3mm,white)); |

|
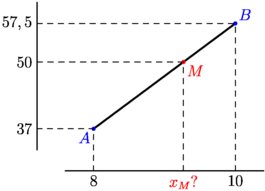
/* Illustration aidant au calcul de la médiane d'une série à caractère quantitatif continu d'après le polygone des effectifs cumulés croissants par interpolation linéaire */ /* Variables à modifier */ // Définition de la taille de l'image size(7cm,5cm,false); // Points A et B définissant l'un des segments du polygone pair A=(8,37),B=(10,57.5); // Ordonnée du point de [AB] dont on cherche l'abscisse real yM=50; /* A priori, ce qui suit ne doit pas être modifié la figure va s'adapter aux valeurs données précédemment */ real xM=(yM-A.y)*(B.x-A.x)/(B.y-A.y)+A.x; real dx=.2(B.x-A.x), dy=.2(B.y-A.y); draw((A.x-dx,A.y-2dy)--(B.x+dx,A.y-2dy),.7bp+black); draw((A.x-2dx,A.y-dy)--(A.x-2dx,B.y+dy),.7bp+black); draw(A--B,1.2bp+black); dot("$A$",A,SW,blue); dot("$B$",B,NE,blue); dot("$M$",(xM,yM),SE,red); draw((A.x-2dx,A.y)--A--(A.x,A.y-2dy),dashed+.5bp+black); draw((A.x-2dx,B.y)--B--(B.x,A.y-2dy),dashed+.5bp+black); draw((A.x-2dx,yM)--(xM,yM)--(xM,A.y-2dy),dashed+.5bp+black); label(format("$%f$",A.x),(A.x,A.y-2dy),S); label(format("$%f$",A.y),(A.x-2dx,A.y),W); label(format("$%f$",B.x),(B.x,A.y-2dy),S); label(format("$%f$",B.y),(A.x-2dx,B.y),W); label("$x_M$?",(xM,A.y-2dy),S,red); label(format("$%f$",yM),(A.x-2dx,yM),W); |

|
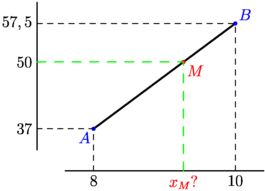
/* Une deuxième façon de faire en exploitant l'extension geometry de Ph.Ivaldi */ import geometry; /* Variables à modifier */ // Définition de la taille de l'image size(7cm,5cm,false); // Points A et B définissant l'un des segments du polygone point A=(8,37),B=(10,57.5); // Ordonnée du point de [AB] dont on cherche l'abscisse real yM=50; /* A priori, ce qui suit ne doit pas être modifié la figure va s'adapter aux valeurs données précédemment */ // définition des axes real dx=.2(B.x-A.x), dy=.2(B.y-A.y); point ptX1=(A.x-dx,A.y-2dy),ptX2=(B.x+dx,A.y-2dy), ptY1=(A.x-2dx,A.y-dy),ptY2=(A.x-2dx,B.y+dy); draw(ptX1--ptX2^^ptY1--ptY2,.7bp+black); // définition des projections sur les axes transform pX = projection(ptX1,ptX2,ptY1,ptY2), pY = projection(ptY1,ptY2,ptX1,ptX2); // Définition du point M de [AB] d'ordonnée yM point M=intersectionpoint(line(A,B),line(0,yM)); draw(A--B,1.2bp+black); dot("$A$",A,SW,blue); dot("$B$",B,NE,blue); dot("$M$",M,SE,red); draw(pX*A--A--pY*A^^pX*B--B--pY*B,dashed+.5bp+black); draw(pX*M--M--pY*M,dashed+.8bp+green); label(format("$%f$",A.x),pX*A,S); label(format("$%f$",A.y),pY*A,W); label(format("$%f$",B.x),pX*B,S); label(format("$%f$",B.y),pY*B,W); label("$x_M$?",pX*M,S,red); label(format("$%f$",yM),pY*M,W); |
Dernière modification le Sat Dec 17 20:45:12 CET 2011 par G.Marris Valide XHTML