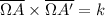Pavages hyperboliques

[GM]

Je lance un sujet sur le thème des "pavages hyperboliques" que je complèterai ensuite.

A l'origine de ce message, un mail de Patrick Fradin (le créateur de l'excellent TeXGraph) sur la liste Syracuse pour attirer notre attention sur ce site :

http://images.math.cnrs.fr/Ringworld.html

et ce que cela lui a inspiré :

http://melusine.eu.org/syracuse/texgraph/exemples/hpavages/

Pour arriver à ce magnifique résultat, la technique n'est pas simple... si vous avez tenté de comprendre le premier lien

et donc Patrick nous a écrit un magnifique document explicatif :

http://dl.dropbox.com/u/7335679/pavages ... liques.pdf

... dont je n'ai encore lu que le tout début et m'a donné envie de réaliser une première figure, en lien avec son document, pour illustrer ce qu'est une droite hyperbolique.

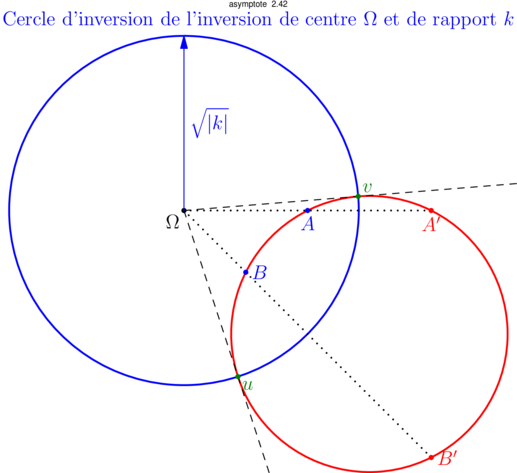
*** Pour masquer/découvrir le code Asymptote qui a permis de créer la figure, il faut cliquer dessus. ;-) ***

CODE ASYMPTOTE de la figure ci-dessus : Tout sélectionner

size(300);
import geometry;
 
point pO=(0,0);
real k=2;
inversion inv=inversion(k,pO);
 
point pA=(1,0), pB=(.5,-.5),
      iA=inv*pA, iB=inv*pB;
 
circle c1=circle(inv),
       c2=circle(pA,pB,iA);
 
draw(c1,linewidth(bp)+blue);
draw(c2,linewidth(bp)+red);
 
point[] uv=intersectionpoints(c1,c2);
point u=uv[0], v=uv[1];
 
line Ou=line(pO,false, u),
     Ov=line(pO,false, v);
 
draw(pO--iA,1bp+dotted);
draw(pO--iB,1bp+dotted);
 
draw(Ou^^Ov,dashed);
 
dot("$\Omega$",pO,SW);
dot("$A$",pA,S,blue);
dot("$A'$",iA,S,red);
dot("$B$",pB,E,blue);
dot("$B'$",iB,E,red);
dot("$u$",u,SE,.5green);
dot("$v$",v,NE,.5green);
 
draw("$\sqrt{|k|}$",pO--pO+sqrt(abs(k))*dir(90),blue,Arrow());
 
label("Cercle d'inversion de l'inversion de centre $\Omega$ et de rapport $k$",truepoint(N),N,blue);

Rappelons à propos de l'inversion :

Si désigne un espace affine euclidien, un point de et un réel non nul, alors, pour tout point de distinct de , il existe un unique point de , tel que :

• , et sont alignés ;
• 

On appelle inversion de centre et de rapport , l'application de dans lui-même qui à associe sous les conditions précédentes.

et aussi que :

• Le cercle d'inversion est le cercle de centre et de rapport est globalement invariant (invariant point par point lorsque ).
• Deux points et leurs images sont cocycliques, sur un cercle orthogonal au cercle d'inversion.

Le plus dur reste à faire.

[GM]

Un cas particulier de l'exemple précédent :

*** Pour masquer/découvrir le code Asymptote qui a permis de créer la figure, il faut cliquer dessus. ;-) ***

CODE ASYMPTOTE de la figure ci-dessus : Tout sélectionner

size(300);
import geometry;
show(defaultcoordsys);
 
point pO=(0,0);
real k=1;
inversion inv=inversion(k,pO);
 
point pA=(.5,.1), pB=(.4,-.3),
      iA=inv*pA, iB=inv*pB;
 
circle c1=circle(inv),
       c2=circle(pA,pB,iA);
 
draw(c1,linewidth(bp)+blue);
 
 
point[] uv=intersectionpoints(c1,c2);
point u=uv[0], v=uv[1];
 
draw((path)arc(c2, v, u),2bp+red);
draw((path)arc(c2, u, v),dashed+red);
 
line Ou=line(pO,false, u),
     Ov=line(pO,false, v);
 
draw(pO--iA,1bp+dotted);
draw(pO--iB,1bp+dotted);
 
draw(Ou^^Ov,dashed);
 
dot("$a$",pA,S,blue);
dot("$\frac1{\overline{a}}$",iA,N,red);
dot("$b$",pB,E,blue);
dot("$\frac1{\overline{b}}$",iB,S,red);
dot("$u$",u,E,.5green);
dot("$v$",v,N,.5green);
 
line tgu=tangent(c1,u), tgv=tangent(c1,v);
draw(tgu^^tgv,.5green+dashed);
dot("$c$",intersectionpoint(tgu,tgv),S);
 
label(scale(.8)*"Cercle d'inversion de l'inversion de centre $O$ et de rapport $k=1$",truepoint(N),N,blue);
label("Inversion d'\'ecriture complexe $z'=\displaystyle\frac{1}{\overline{z}}$",truepoint(S),S);

[GM]

J'ai poursuivi un peu la lecture du document de Patrick (qui explique les notions utiles à la pratique du pavage hyperbolique),

et après avoir parlé de droites hyperboliques, il effectue un rappel sur la notion d'isométrie hyperbolique et en particulier, sur la notion de rotation hyperbolique.

Un exemple avec Asymptote :

*** Pour masquer/découvrir le code Asymptote qui a permis de créer la figure, il faut cliquer dessus. ;-) ***

CODE ASYMPTOTE de la figure ci-dessus : Tout sélectionner

size(300);
import geometry;
show(defaultcoordsys);
 
point pO=(0,0);
real k=1, theta=120;
inversion inv=inversion(k,pO);
 
 
point pA=(.4,-.2), pB=(.7,.3), iA=inv*pA;
 
// T : z'=(z+a)/(1+conj(a)z)
pair T(pair z) {return (z+pA)/(1+conj(pA)*z);}
// T^{-1} : z=(z'-a)/(1-z'conj(a))
pair rT(pair z) {return (z-pA)/(1-conj(pA)*z);}
 
// La rotation hyperbolique R(A,theta) est la composée de :
// T^{-1} 
// suivie de rotation hyperbolique (et euclidienne !) R(0,theta)
// suivie de T
point pBp=T(rotate(theta)*rT(pB));
 
circle c1=circle(inv),
       c2=circle(pA,pB,iA),
	   c3=circle(pA,pBp,iA);
 
draw(c1,linewidth(bp)+blue);
clipdraw(c2, 0.8*red+dashed);
clipdraw(c3, 0.8*red+dashed);
 
arc arc1=arc(c2,pB,pA), arc2=arc(c3,pA,pBp);
draw(arc1,2bp+red);
draw(arc2,2bp+red);
 
dot("$A(a)$",pA,SE,red);
dot("$B(b)$",pB,E,blue);
dot("$B'(b')$",pBp,S,blue);
 
 
point pM=pA-.5dir(arc1,reltime(arc1,1)),
      pN=pA+.5dir(arc2,0);
draw(pA--pM,red);
draw(pA--pN,red);
markangle("$\theta$",pM,pA,pN,grey);
 
label(scale(.8)*"Rotation hyperbolique de centre $A(a)$, d'angle $\theta$",truepoint(S),S);

La même figure mais avec une variante de code (qui exploite des matrices, comme évoquées dans le rappel qui suit) :

*** Pour masquer/découvrir le code Asymptote qui a permis de créer la figure, il faut cliquer dessus. ;-) ***

CODE ASYMPTOTE de la figure ci-dessus : Tout sélectionner

size(250);
import geometry;
show(defaultcoordsys);
 
point pO=(0,0);
real k=1, theta=120;
inversion inv=inversion(k,pO);
 
pair pA=(.4,-.2), pB=(.7,.3), iA=inv*pA;
real theta=120;
 
pair[][] mat1={{1,-pA},{-conj(pA),1}},
         mat2={{rotate(theta/2)*I,0},{0,rotate(-theta/2)*I}},
		 mat3={{1,pA},{conj(pA),1}},
		 mat=mat3*mat2*mat1;
 
pair f(pair z) {return (mat[0][0]*z+mat[0][1])/(mat[1][0]*z+mat[1][1]);}
 
circle c1=circle(inv),
       c2=circle(pA,pB,iA),
	   c3=circle(pA,f(pB),iA);
 
draw(c1,linewidth(bp)+blue);
clipdraw(c2, 0.8*red+dashed);
clipdraw(c3, 0.8*red+dashed);
 
arc arc1=arc(c2,pB,pA), arc2=arc(c3,pA,f(pB));
draw(arc1,2bp+red);
draw(arc2,2bp+red);
 
dot("$A(a)$",pA,SE,red);
dot("$B(b)$",pB,E,blue);
dot("$B'(b')$",f(pB),S,blue);
 
 
point pM=pA-.5dir(arc1,reltime(arc1,1)),
      pN=pA+.5dir(arc2,0);
draw(pA--pM,red);
draw(pA--pN,red);
markangle("$\theta$",pM,pA,pN,grey);
 
label(scale(.8)*"Rotation hyperbolique de centre $A(a)$, d'angle $\theta$",truepoint(S),S);

2010-07-06_021040.png (17.03 Kio) Vu 9642 fois

On se rapproche... toujours un peu plus... des premiers pavages hyperboliques.

[OG]

Bonjour

As-tu regardé le paquet de géométrie hyperbolique de R. Bourquin ?
http://raoul.koalatux.ch/sites/hyperbol ... metry.html

Voir les exemples sur sa page.

O.G.

[GM]

As-tu regardé le paquet de géométrie hyperbolique de R. Bourquin ?
http://raoul.koalatux.ch/sites/hyperbol ... metry.html

ahh, bein non... je ne savais pas que cela existait.