Figures de bac

[Nico56]

Bonsoir, je vous propose des figures issues des documents de l'APMEP que j'ai retranscrites en asymptote.
Il est probable que les codes ne soient pas optimisés, mais cela me suffit.

2014 - septembre - Antilles et Guyane :

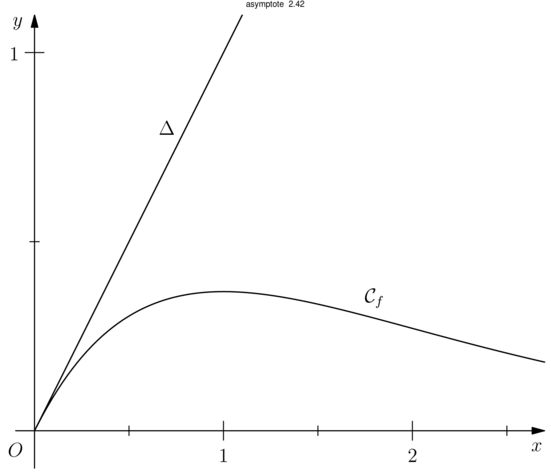
*** Pour masquer/découvrir le code Asymptote qui a permis de créer la figure, il faut cliquer dessus. ;-) ***

CODE ASYMPTOTE de la figure ci-dessus : Tout sélectionner

import graph_pi;
graphicrules(xunit=4cm, yunit=8cm, xmin=-0.1, xmax=2.7, ymin=-0.1, ymax=1.1);
cartesianaxis(extraheight=0,extrawidth=0,
              xticks=Ticks(Step=1,step=0.5,NoZero), 
              yticks=Ticks(Step=1,step=0.5,NoZero)
             );
 
real f(real t) {return t/exp(t);}
path Cf=graph(f,0.01,2.7,n=100);
draw(Cf,linewidth(0.75bp));
label("$\mathcal{C}_{f}$",(1.8,0.35));
 
real g(real t) {return t;}
path Cg=graph(g,0,1.1,n=2);
draw(Cg,linewidth(0.75bp));
label("$\Delta$",(0.7,0.8));
 
label("$O$",(-0.1,-0.05));
 
ylimits(-0.1,1.1,Crop);
shipout(bbox(0.1cm,0.1cm,invisible));

Le corrigé :

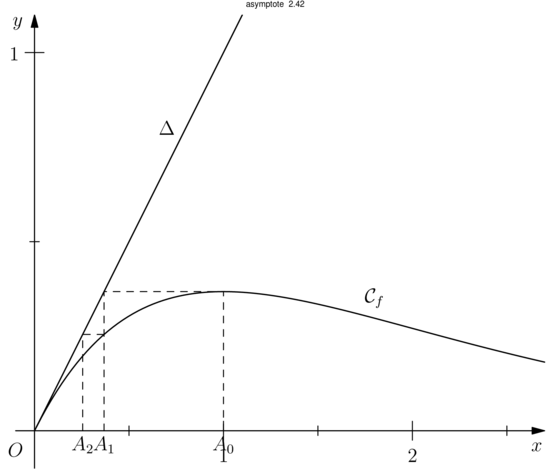
*** Pour masquer/découvrir le code Asymptote qui a permis de créer la figure, il faut cliquer dessus. ;-) ***

CODE ASYMPTOTE de la figure ci-dessus : Tout sélectionner

import graph_pi;
graphicrules(xunit=4cm, yunit=8cm, xmin=-0.1, xmax=2.7, ymin=-0.1, ymax=1.1);
cartesianaxis(extraheight=0,extrawidth=0,
              xticks=Ticks(Step=1,step=0.5,NoZero), 
              yticks=Ticks(Step=1,step=0.5,NoZero)
             );
real f(real t) {return t/exp(t);}
path Cf=graph(f,0.01,2.7,n=100);
draw(Cf,linewidth(0.75bp));
label("$\mathcal{C}_{f}$",(1.8,0.35));
 
real g(real t) {return t;}
path Cg=graph(g,0,1.1,n=2);
draw(Cg,linewidth(0.75bp));
label("$\Delta$",(0.7,0.8));
 
label("$O$",(-0.1,-0.05));
 
pair A,B,C,fA,ffA,fB,ffB;
A=(1,0);
fA=(1,f(1));
ffA=(f(1),f(1));
B=(f(1),0);
fB=(f(1),f(f(1)));
ffB=(f(f(1)),f(f(1)));
C=(f(f(1)),0);
 
draw(A--fA--ffA--B, dashed);
draw(fB--ffB--C, dashed);
 
label("$A_0$",A,S);
label("$A_1$",B,S);
label("$A_2$",C,S);
 
ylimits(-0.1,1.1,Crop);
shipout(bbox(0.1cm,0.1cm,invisible));

2014 - Amérique du Nord - Exercice 2 :

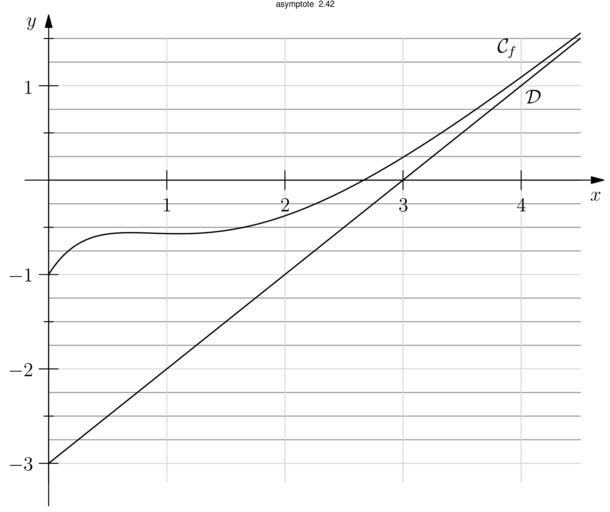
*** Pour masquer/découvrir le code Asymptote qui a permis de créer la figure, il faut cliquer dessus. ;-) ***

CODE ASYMPTOTE de la figure ci-dessus : Tout sélectionner

import graph_pi;
 
graphicrules(xunit=2.5cm, yunit=2cm, xmin=0, xmax=4.5, ymin=-3.2, ymax=1.5);
grid(pTick=gray(0.8),xmin=0,xstep=0,ystep=0.25); //,ptick=gray(0.8)
 
cartesianaxis(extraheight=1,extrawidth=1,
              xticks=Ticks(Step=1,step=0,NoZero),
              yticks=Ticks(Step=1,step=0.5,NoZero)
             );
 
real f(real t){return 5*exp(-t)-3*exp(-2t)+t-3;}
path Cf=graph(f,0,4.5,n=300);
draw(Cf,linewidth(0.75bp));
 
real g(real t){return t-3;}
path Cg=graph(g,0,4.5,n=2);
draw(Cg,linewidth(0.75bp));
 
label("$\mathcal{C}_f$",(4,1.25),NW);
label("$\mathcal{D}$",(4,1),SE);
 
shipout(bbox(0.1cm,0.1cm,invisible));

2014 - Amérique du Sud - Exercice 4, figure 1:

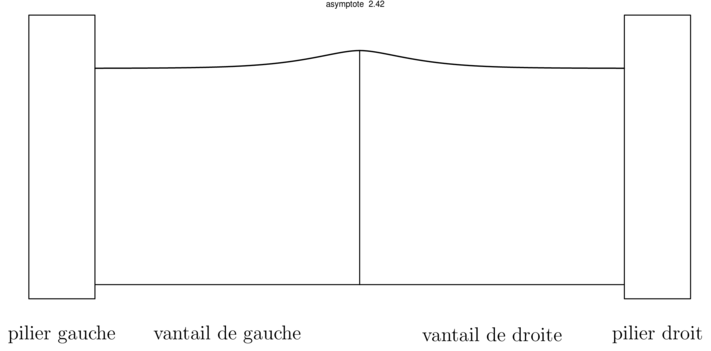
*** Pour masquer/découvrir le code Asymptote qui a permis de créer la figure, il faut cliquer dessus. ;-) ***

CODE ASYMPTOTE de la figure ci-dessus : Tout sélectionner

unitsize(2.8cm,1.5cm);
import graph;
real f(real t){return (t+0.25)*exp(-4t)+1.25;}
path Cf=graph(f,0,2,n=300);
draw(Cf,linewidth(0.75bp));
real g(real t){return (-t+0.25)*exp(4t)+1.25;}
path Cg=graph(g,-2,0,n=300);
draw(Cg,linewidth(0.75bp));
draw((-2.5,-2)--(-2,-2)--(-2,2)--(-2.5,2)--cycle);
draw(shift(4.5,0)*((-2.5,-2)--(-2,-2)--(-2,2)--(-2.5,2)--cycle));
label("pilier gauche",(-2.25,-2.5));
label("pilier droit",(2.25,-2.5));
label("vantail de gauche",(-1,-2.5));
label("vantail de droite",(1,-2.5));
draw((0,-1.8)--(0,1.5));
draw((-2,-1.8)--(2,-1.8));
shipout(bbox(0.1cm,0.1cm,invisible));

Figure 2 :

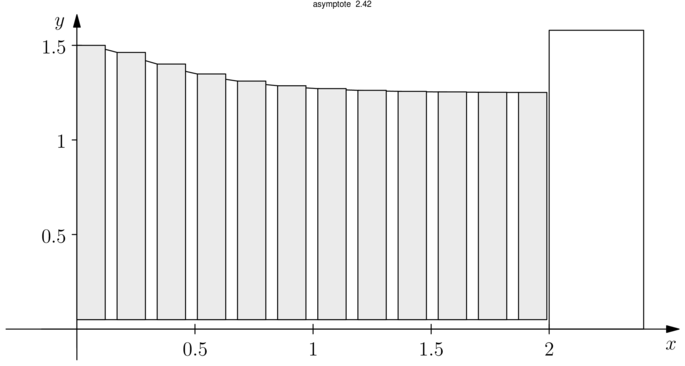
*** Pour masquer/découvrir le code Asymptote qui a permis de créer la figure, il faut cliquer dessus. ;-) ***

CODE ASYMPTOTE de la figure ci-dessus : Tout sélectionner

import graph_pi;
graphicrules(xunit=5cm, yunit=4cm, xmin=-0.15, xmax=2.4,ymin=-0.1, ymax=1.6);
cartesianaxis(extraheight=.5,extrawidth=1.5,
              xticks=Ticks(Step=0.5,step=0,NoZero,Size=1mm),
              yticks=Ticks(Step=0.5,step=0,NoZero,Size=1mm)
             );
 
real f(real t) {return (t+0.25)*exp(-4t)+1.25;}
path Cf=graph(f,0,1.87,n=100);
draw(Cf);
 
real larg=.12, esp=.05, lx = larg+esp;
draw((0,esp)--(1.87,esp));
 
for (int i=0; i<=11; ++i){
   filldraw((lx*i,esp)--(lx*i,f(i*lx))--(larg+lx*i,f(i*lx))--(larg+lx*i,esp)--cycle,lightgray);
}
 
draw((2,1.58)--(2,0)--(2.4,0)--(2.4,1.58)--(2,1.58));
 
shipout(bbox(0.1cm,0.1cm,invisible));

2014- Pondichéry - Exercice 4, figure 1 :

*** Pour masquer/découvrir le code Asymptote qui a permis de créer la figure, il faut cliquer dessus. ;-) ***

CODE ASYMPTOTE de la figure ci-dessus : Tout sélectionner

import graph_pi;
 
graphicrules(xunit=0.7cm, yunit=0.7cm, xmin=-3, xmax=5,ymin=-2, ymax=10);
cartesianaxis(extraheight=0,extrawidth=0,
              xticks=Ticks(scale(.7)*Label(),Step=1,step=0,NoZero,end=false,endlabel=false,begin=false,beginlabel=false,Size=1mm),
              yticks=Ticks(scale(.7)*Label(),Step=1,step=0,NoZero,end=false,endlabel=false,begin=false,beginlabel=false,Size=1mm)
             );
grid(pTick=gray(0.8),xstep=0,ystep=0); //,ptick=gray(0.8)
 
real f(real t) {return 2t+1+exp(-t);}
path Cf=graph(f,-3,4.5,n=300);
draw(Cf,linewidth(0.75bp));
label("$\mathcal{C}_{1}$",(-2.5,8),E);
 
real[] xpt={-1.5,-1,0,1,2,3,4,4.5};
real[] ypt={-2.2,-0.8,1,1.6,1.85,1.95,2,1.98};
 
draw(graph(xpt,ypt,Hermite(monotonic)),linewidth(0.75bp));
label("$\mathcal{C}_{2}$",(3,2),N);
ylimits(-2,10,Crop);
shipout(bbox(0.1cm,0.1cm,invisible));

Figure 2 :

*** Pour masquer/découvrir le code Asymptote qui a permis de créer la figure, il faut cliquer dessus. ;-) ***

CODE ASYMPTOTE de la figure ci-dessus : Tout sélectionner

import graph_pi;
 
graphicrules(xunit=0.7cm, yunit=0.7cm, xmin=-3, xmax=5,ymin=-2, ymax=10);
cartesianaxis(extraheight=0,extrawidth=0,
              xticks=Ticks(scale(.7)*Label(),Step=1,step=0,NoZero,end=false,endlabel=false,begin=false,beginlabel=false,Size=1mm), 
              yticks=Ticks(scale(.7)*Label(),Step=1,step=0,NoZero,end=false,endlabel=false,begin=false,beginlabel=false,Size=1mm)
             );
grid(pTick=gray(0.8),xstep=0,ystep=0); //,ptick=gray(0.8)
 
real f(real t) {return 2t+1+exp(-t);}
path Cf=graph(f,-3,4.5,n=300);
draw(Cf,linewidth(0.75bp));
label("$\mathcal{C}_{1}$",(-2.5,8),E);
 
real g(real t) {return t+1;}
path Cg=graph(g,-3,5,n=2);
draw(Cg,linewidth(0.75bp));
label("$\mathcal{C}_{2}$",(4,5),SE);
 
ylimits(-2,10,Crop);
shipout(bbox(0.1cm,0.1cm,invisible));

Figure 3 :

*** Pour masquer/découvrir le code Asymptote qui a permis de créer la figure, il faut cliquer dessus. ;-) ***

CODE ASYMPTOTE de la figure ci-dessus : Tout sélectionner

import graph_pi;
 
graphicrules(xunit=0.7cm, yunit=0.7cm, xmin=-3, xmax=5,ymin=-2, ymax=10);
cartesianaxis(extraheight=0,extrawidth=0,
              xticks=Ticks(scale(.7)*Label(),Step=1,step=0,NoZero,end=false,endlabel=false,begin=false,beginlabel=false,Size=1mm), 
              yticks=Ticks(scale(.7)*Label(),Step=1,step=0,NoZero,end=false,endlabel=false,begin=false,beginlabel=false,Size=1mm)
             );
grid(pTick=gray(0.8),xstep=0,ystep=0); //,ptick=gray(0.8)
 
real f(real t) {return 2t+1+exp(-t);}
path Cf=graph(f,-3,4.5,n=300);
draw(Cf,linewidth(0.75bp));
label("$\mathcal{C}_{1}$",(-2.5,8),E);
 
real g(real t) {return 2t+exp(-t);}
path Cg=graph(g,-3,5,n=300);
draw(Cg,linewidth(0.75bp));
label("$\mathcal{C}_{2}$",(3,6),SE);
 
ylimits(-2,10,Crop);
shipout(bbox(0.1cm,0.1cm,invisible));

Figure 4 :

*** Pour masquer/découvrir le code Asymptote qui a permis de créer la figure, il faut cliquer dessus. ;-) ***

CODE ASYMPTOTE de la figure ci-dessus : Tout sélectionner

import graph_pi;
 
graphicrules(xunit=0.8cm, yunit=0.8cm, xmin=-2, xmax=2,ymin=-1, ymax=6);
 
real f(real t) {return 2t+1+exp(-t);}
path Cf=graph(f,-2,2,n=300);
draw(Cf,linewidth(0.5bp));
 
real g(real t) {return t+2;}
path Cg=graph(g,-2,2,n=2);
draw(Cg,linewidth(0.5bp));
 
draw((-2,0)--(2,0)--(2,f(2))--(-2,f(-2))--(-2,0));
fill((graph(f,-2,2))--(2,4)--(-2,0)--cycle,lightblue+opacity(.3));
 
ylimits(-1,6,Crop);
shipout(bbox(0.1cm,0.1cm,invisible));

Figure 5 :

*** Pour masquer/découvrir le code Asymptote qui a permis de créer la figure, il faut cliquer dessus. ;-) ***

CODE ASYMPTOTE de la figure ci-dessus : Tout sélectionner

import graph_pi;
 
graphicrules(xunit=0.8cm, yunit=0.8cm, xmin=-3, xmax=3, ymin=-1, ymax=6);
cartesianaxis(extraheight=0,extrawidth=1,
              xticks=Ticks("%",step=1,Size=.5mm), 
              yticks=Ticks("%",step=1,Size=.5mm),
              arrow=None);
labeloij(p=currentpen);
 
real f(real t) {return 2t+1+exp(-t);}
path Cf=graph(f,-2,2,n=300);
draw(Cf,linewidth(0.5bp));
 
real g(real t) {return t+2;}
path Cg=graph(g,-2,2,n=2);
draw(Cg,linewidth(0.5bp));
 
draw((-2,0)--(2,0)--(2,f(2))--(-2,f(-2))--(-2,0));
fill((graph(f,-2,2))--(2,4)--(-2,0)--cycle,lightblue+opacity(.3));
 
label("$D$",(-2,0),S);
label("$E$",(2,0),S);
label("$F$",(2,f(2)),NE);
label("$G$",(-2,f(-2)),NW);
ylimits(-1,6,Crop);
shipout(bbox(0.1cm,0.1cm,invisible));