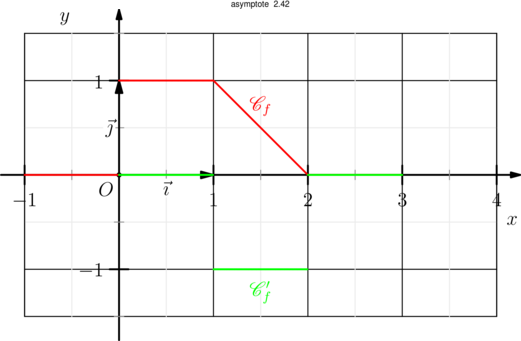
Non tracé des discontinuités
Où est mon erreur alors ?
Code : Tout sélectionner
import graph;
size(300);
real xmin=-3,xmax=3;
real ymin=-1,ymax=2;
// Test pour savoir s'il faut relier les points ou pas lors de l'utilisation de graph.
bool3 condition(real x)
{
static int derniersigne=0;
int signe = sgn(x);
bool b = derniersigne == 0 || signe == derniersigne;
derniersigne = signe;
return b ? true : default;
}
// Définition de la fonction de Heaviside
real H(real t) {return t < 0 ? 0 : 1;}
// Définition de la fonction
real f(real t){ return t*H(t)-(t-1)*H(t-1)-H(t-2);}
// Tracé de la courbe
guide[] CH=graph(f,xmin,xmax,condition,n=400);
draw(CH,1.5bp+blue);
real margeaxe=.4;
xaxis(Label("$x$",align=Align),xmin-margeaxe,xmax+margeaxe,Ticks(NoZero),Arrow);
yaxis(ymin-margeaxe,ymax+margeaxe,Ticks(NoZero),Arrow);
shipout(bbox(2mm,Fill(white)));