J'ai le problème suivant :
Je voudrais tracer la suite de fonctions
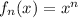 (
( ![x\in [0,1] x\in [0,1]](/forum/latexrender/pictures/c628ba2b1047de93f66cb815d986e107.png) ) pour
) pour 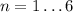 .
.Pour différentes valeurs de
 , je voudrais positionner les graphes comme dans l'image ci-dessous.
, je voudrais positionner les graphes comme dans l'image ci-dessous.Quelqu'un a une idée?
Merci
Toufan
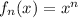 (
( ![x\in [0,1] x\in [0,1]](/forum/latexrender/pictures/c628ba2b1047de93f66cb815d986e107.png) ) pour
) pour 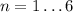 .
. , je voudrais positionner les graphes comme dans l'image ci-dessous.
, je voudrais positionner les graphes comme dans l'image ci-dessous.Code : Tout sélectionner
//Plusieurs graphes sur une même figure.
import graph;
picture pic1,pic2,pic3,pic4;
//La fonction
real f(real x){
return 5exp(-5x)*cos(60x);
}
//Le tracé de la fig1
size(pic1,6cm,4cm,IgnoreAspect);
draw(pic1,graph(f, 0, .8), red+2);
add(pic1.fit(),(0,0),W);
//Le tracé de la fig2
size(pic2,6cm,4cm,IgnoreAspect);
draw(pic2,graph(f, 0, .8), blue+2);
add(pic2.fit(),(5mm,0),E);
//Le tracé de la fig3
size(pic3,6cm,4cm,IgnoreAspect);
draw(pic3,graph(f, 0, .8), green+2);
add(pic3.fit(),(0,-2cm),SW);
//Le tracé de la fig4
size(pic4,6cm,4cm,IgnoreAspect);
draw(pic4,graph(f, 0, .8), black+2);
add(pic4.fit(),(5mm,-2cm),SE);
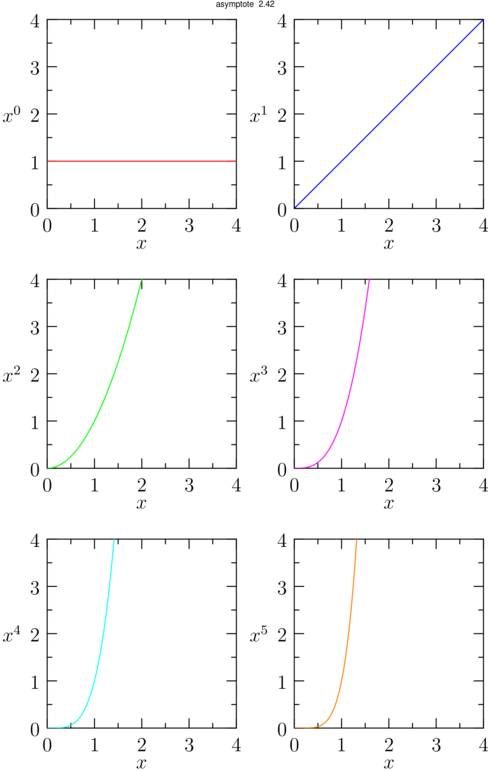
*** Pour masquer/découvrir le code Asymptote qui a permis de créer la figure, il faut cliquer dessus. ;-) ***
- import graph;
-
- unitsize(1cm);
-
- typedef real fonction_avec_parametre(real);
-
- fonction_avec_parametre F(real n) {
- return new real(real x) {return x^n;};
- };
-
-
- picture fonction_puissance_n(int n) {
- picture pic;
- unitsize(pic,1cm);
- draw(pic,graph(F(n),0,4),Pen(n));
- limits(pic,(0,0),(4,4),Crop);
- xaxis(pic,"$x$",BottomTop,LeftTicks);
- yaxis(pic,format("$x^%i$",n),LeftRight,RightTicks(trailingzero));
- return pic;
- }
-
- real ev=5.5;
- for(int i=0; i < 3; ++i){
- add(fonction_puissance_n(2*i).fit(),(0,-i*ev),W);
- add(fonction_puissance_n(2*i+1).fit(),(0,-i*ev),E);
- }
-
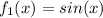 sur
sur ![[0; 3\pi] [0; 3\pi]](/forum/latexrender/pictures/801fab100135d67a90f5cfff0d426590.png)
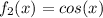 sur
sur ![[-\pi; 3\pi] [-\pi; 3\pi]](/forum/latexrender/pictures/6b9aa0cbdc83ffbb16acda46b6e1e9c7.png)
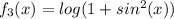 sur
sur ![[-2\pi; 5\pi] [-2\pi; 5\pi]](/forum/latexrender/pictures/99bedb1f3189b3ff5f664a0b8062fd1e.png)
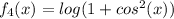 sur
sur ![[-3\pi; \pi] [-3\pi; \pi]](/forum/latexrender/pictures/36095a2654b7dab4cfef05bac093add5.png)
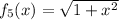 sur
sur ![[-2; 7] [-2; 7]](/forum/latexrender/pictures/8d00ba384768601bceb5a3c16e9678bf.png)
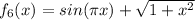 sur
sur ![[-1; 1] [-1; 1]](/forum/latexrender/pictures/ceb10625c9bc04a2faeb343e7f5a2698.png)
![ListeFonction[0]=f_1(x) , .... , ListeFonction[5]=f_6(x) ListeFonction[0]=f_1(x) , .... , ListeFonction[5]=f_6(x)](/forum/latexrender/pictures/c8468fac631c8e9c32b1693ae506fa20.png)
![ListeDomaine[0]=pair (0, 3\pi) , .... , ListeDomaine[5]=pair (-1, 1) ListeDomaine[0]=pair (0, 3\pi) , .... , ListeDomaine[5]=pair (-1, 1)](/forum/latexrender/pictures/91ad6c31eb7b32b37cedfcc8a3c048a3.png)
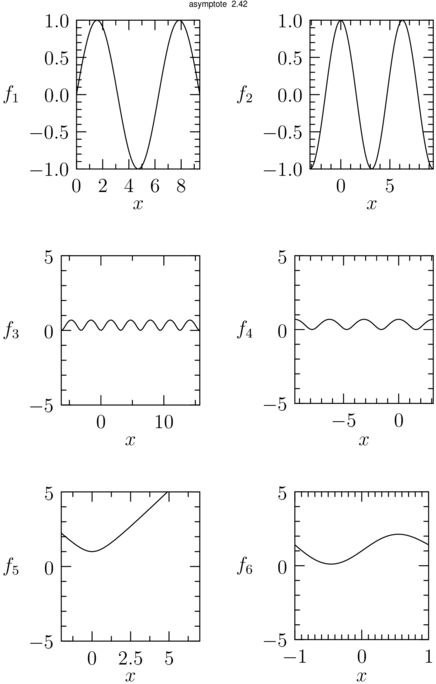
*** Pour masquer/découvrir le code Asymptote qui a permis de créer la figure, il faut cliquer dessus. ;-) ***
- import graph;
-
- unitsize(1cm);
-
- struct FONCTION{
- string n;
- real expr(real);
- real xmin;
- real xmax;
- real ymin;
- real ymax;
- void operator init(string n="",
- real expr(real),
- real xmin,
- real xmax,
- real ymin=-5,
- real ymax=5)
- {
- this.n=n;
- this.expr=expr;
- this.xmin=xmin;
- this.xmax=xmax;
- this.ymin=ymin;
- this.ymax=ymax;
- }
- }
-
- FONCTION f1=FONCTION("$f_1$",new real(real x) {return sin(x);}, 0, 3pi, -1, 1),
- f2=FONCTION("$f_2$",new real(real x) {return cos(x);}, -pi, 3pi, -1, 1),
- f3=FONCTION("$f_3$",new real(real x) {return log(1+(sin(x))^2);}, -2pi, 5pi),
- f4=FONCTION("$f_4$",new real(real x) {return log(1+(cos(x))^2);}, -3pi, pi),
- f5=FONCTION("$f_5$",new real(real x) {return sqrt(1+x^2);}, -2, 7),
- f6=FONCTION("$f_6$",new real(real x) {return sin(pi*x)+f5.expr(x);}, -1, 1);
-
- FONCTION[] f={f1,f2,f3,f4,f5,f6} ;
-
- picture courbefonction(FONCTION f) {
- picture pic;
- size(pic,120,120,false);
- draw(pic,graph(f.expr,f.xmin,f.xmax));
- limits(pic,(f.xmin,f.ymin),(f.xmax,f.ymax),Crop);
- xaxis(pic,"$x$",BottomTop,LeftTicks);
- yaxis(pic,f.n,LeftRight,RightTicks(trailingzero));
- return pic;
- }
-
- real eh=10, ev=5;
- for(int i=0; i < 3; ++i){
- add(courbefonction(f[2*i]).fit(),(0,-i*ev),eh*W);
- add(courbefonction(f[2*i+1]).fit(),(0,-i*ev),eh*E);
- }
-
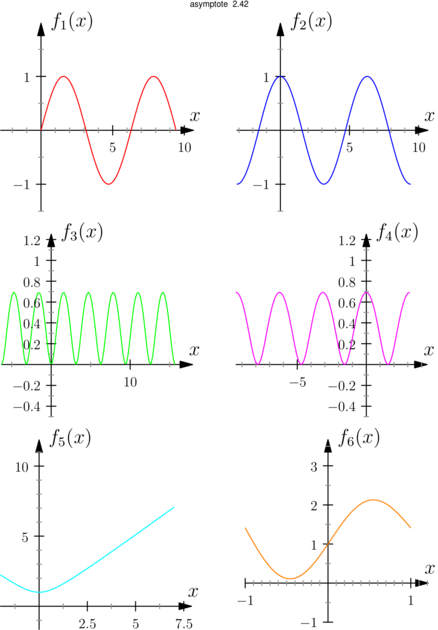
*** Pour masquer/découvrir le code Asymptote qui a permis de créer la figure, il faut cliquer dessus. ;-) ***
- import graph;
-
- unitsize(1cm);
-
- struct FONCTION{
- string n;
- real expr(real);
- real xmin;
- real xmax;
- real ymin;
- real ymax;
- void operator init(string n="",
- real expr(real),
- real xmin,
- real xmax,
- real ymin=-5,
- real ymax=5)
- {
- this.n=n;
- this.expr=expr;
- this.xmin=xmin;
- this.xmax=xmax;
- this.ymin=ymin;
- this.ymax=ymax;
- }
- }
-
- FONCTION f1=FONCTION("$f_1(x)$",new real(real x) {return sin(x);}, 0, 3pi, -1.5, 1.5),
- f2=FONCTION("$f_2(x)$",new real(real x) {return cos(x);}, -pi, 3pi, -1.5, 1.5),
- f3=FONCTION("$f_3(x)$",new real(real x) {return log(1+(sin(x))^2);}, -2pi, 5pi, -.5, 1),
- f4=FONCTION("$f_4(x)$",new real(real x) {return log(1+(cos(x))^2);}, -3pi, pi, -.5, 1),
- f5=FONCTION("$f_5(x)$",new real(real x) {return sqrt(1+x^2);}, -2, 7, 0, 10),
- f6=FONCTION("$f_6(x)$",new real(real x) {return sin(pi*x)+f5.expr(x);}, -1, 1, -1, 3);
-
- FONCTION[] f={f1,f2,f3,f4,f5,f6} ;
-
- picture courbefonction(FONCTION f, pen p) {
- picture pic;
- size(pic,120,120,false);
- draw(pic,graph(f.expr,f.xmin,f.xmax),p);
- limits(pic,(f.xmin,f.ymin),(f.xmax,f.ymax),Crop);
- xaxis(pic,Label("$x$",EndPoint,NE),
- Ticks(scale(.7)*Label(align=E),NoZero,Size=1mm, size=.5mm,pTick=black,ptick=gray),
- Arrow);
- yaxis(pic,Label(f.n,EndPoint,NE),
- Ticks(scale(.7)*Label(align=W),NoZero,Size=1mm, size=.5mm,pTick=black,ptick=gray),
- Arrow,autorotate=false);
- return pic;
- }
-
- real eh=10, ev=5;
- for(int i=0; i < 3; ++i){
- picture pic;
- add(pic,courbefonction(f[2*i],Pen(2*i)).fit(),(0,0),eh*W);
- add(pic,courbefonction(f[2*i+1],Pen(2*i+1)).fit(),(0,0),eh*E);
- add(pic.fit(),truepoint(S),ev*S);
- }
-
GM a écrit :Quelque chose comme cela ?
Code : Tout sélectionner
newplot --- > figure 1
draw(pic,graph(f1.expr,f1.xmin,f1.xmax));
....
....
newplot --- > figure 6
draw(pic,graph(f6.expr,f6.xmin,f6.xmax));
GM a écrit :Une petite variante.
au delà du changement esthétique, à noter la modification de la fin du code... qui me semble mieux.
DGH a écrit :Je vais pousser le problème plus loin. Est-il possible de produire les graphes de six fonctions à partir d'un seul code ?
Je vais expliquer , je cherche une commande qu'on note newplot qui crée une nouvelle figure. Quelque chose comme :Code : Tout sélectionner
newplot --- > figure 1
draw(pic,graph(f1.expr,f1.xmin,f1.xmax));
....
....
newplot --- > figure 6
draw(pic,graph(f6.expr,f6.xmin,f6.xmax));
Code : Tout sélectionner
import graph;
unitsize(1cm);
////////////////////////////////////////////////
// Une structure pour définir des fonctions
////////////////////////////////////////////////
struct FONCTION{
string n;
real expr(real);
real xmin;
real xmax;
real ymin;
real ymax;
void operator init(string n="",
real expr(real),
real xmin,
real xmax,
real ymin=-5,
real ymax=5)
{
this.n=n;
this.expr=expr;
this.xmin=xmin;
this.xmax=xmax;
this.ymin=ymin;
this.ymax=ymax;
}
}
FONCTION f1=FONCTION("$f_1(x)$",new real(real x) {return sin(x);}, 0, 3pi, -1.5, 1.5),
f2=FONCTION("$f_2(x)$",new real(real x) {return cos(x);}, -pi, 3pi, -1.5, 1.5),
f3=FONCTION("$f_3(x)$",new real(real x) {return log(1+(sin(x))^2);}, -2pi, 5pi, -.5, 1),
f4=FONCTION("$f_4(x)$",new real(real x) {return log(1+(cos(x))^2);}, -3pi, pi, -.5, 1),
f5=FONCTION("$f_5(x)$",new real(real x) {return sqrt(1+x^2);}, -2, 7, 0, 10),
f6=FONCTION("$f_6(x)$",new real(real x) {return sin(pi*x)+f5.expr(x);}, -1, 1, -1, 3);
FONCTION[] f={f1,f2,f3,f4,f5,f6};
size(120,120,false);
///////////////////////
// Figure 1
///////////////////////
draw(graph(f1.expr,f1.xmin,f1.xmax),red);
limits((f1.xmin,f1.ymin),(f1.xmax,f1.ymax),Crop);
xaxis(Label("$x$",EndPoint,NE),
Ticks(scale(.7)*Label(align=E),NoZero,Size=1mm, size=.5mm,pTick=black,ptick=gray),
Arrow);
yaxis(Label(f1.n,EndPoint,NE),
Ticks(scale(.7)*Label(align=W),NoZero,Size=1mm, size=.5mm,pTick=black,ptick=gray),
Arrow,autorotate=false);
shipout(prefix="figure_1");
erase();
///////////////////////
// Figure 2
///////////////////////
draw(graph(f2.expr,f2.xmin,f2.xmax),red);
limits((f2.xmin,f2.ymin),(f2.xmax,f2.ymax),Crop);
xaxis(Label("$x$",EndPoint,NE),
Ticks(scale(.7)*Label(align=E),NoZero,Size=1mm, size=.5mm,pTick=black,ptick=gray),
Arrow);
yaxis(Label(f2.n,EndPoint,NE),
Ticks(scale(.7)*Label(align=W),NoZero,Size=1mm, size=.5mm,pTick=black,ptick=gray),
Arrow,autorotate=false);
shipout(prefix="figure_2");
Code : Tout sélectionner
add(courbefonction(f1,red).fit());
shipout(prefix="figure_1");
erase();
add(courbefonction(f2,blue).fit());
shipout(prefix="figure_2");