Page 1 sur 5
Surface p-V-T d'un corps pur
Posté : lun. 26 avr. 2010, 12:37
par cjorssen
Bonjour à tous,
Je cherche à reproduire la figure suivante
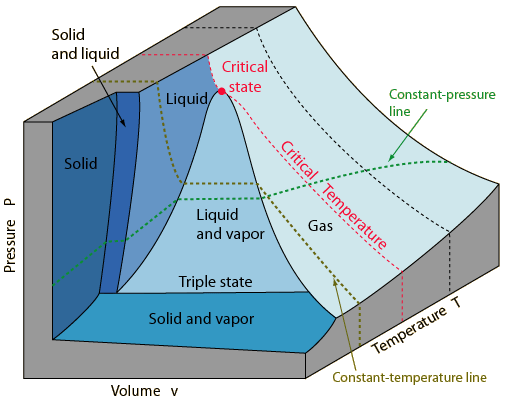
(source :
http://hyperphysics.phy-astr.gsu.edu/Hbase/thermo/pvtsur.html). Je ne sais pas encore où trouver les données expérimentales et/ou les expressions analytiques qu'il me faut (
http://www.eng.usf.edu/~campbell/ThermoI/Proptut/tut1.html), mais j'aimerais savoir s'il sera possible (et comment il faut prévoir la chose au niveau de l'implémentation) d'obtenir les projections des "frontières" sur les plans (p,V), (p,T) et (V,T).
Merci d'avance
--
Christophe
Re: Surface p-V-T d'un corps pur
Posté : lun. 26 avr. 2010, 13:46
par GM
cjorssen a écrit :mais j'aimerais savoir s'il sera possible (et comment il faut prévoir la chose au niveau de l'implémentation) d'obtenir les projections des "frontières" sur les plans (p,V), (p,T) et (V,T).
On sait projeter un path3 sur un plan, ainsi :
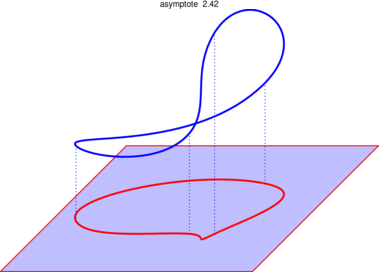
*** Pour masquer/découvrir le code Asymptote qui a permis de créer la figure, il faut cliquer dessus. ;-) ***
- CODE ASYMPTOTE de la figure ci-dessus :
Tout sélectionner
import three;
size(8cm,0);
currentprojection=obliqueX;
currentlight=nolight;
triple v1=(10,0,0),
v2=(0,10,0),
pO=(-2,-3,0);
path3 pl1=plane(v1,v2,pO);
path3 ch=(5,3,4)..(5,4,8)..(1,4,4)..(4,-2,3)..cycle;
transform3 proj=planeproject(pl1);
path3 chproj=proj*ch;
draw(surface(pl1),paleblue+opacity(.5),red);
draw(ch,1bp+blue);
draw(chproj,1bp+red);
for (int i=0; i < length(ch); ++i)
draw(point(ch,i)--point(chproj,i), .5bp+blue+dotted);
Re: Surface p-V-T d'un corps pur
Posté : lun. 26 avr. 2010, 13:54
par GM
Un autre exemple d'utilisation de planeproject : celui de la galerie officielle de JCBowman.

*** Pour masquer/découvrir le code Asymptote qui a permis de créer la figure, il faut cliquer dessus. ;-) ***
- CODE ASYMPTOTE de la figure ci-dessus :
Tout sélectionner
import graph3;
size3(200,IgnoreAspect);
currentprojection=orthographic(4,6,3);
real x(real t) {return 1+cos(2pi*t);}
real y(real t) {return 1+sin(2pi*t);}
real z(real t) {return t;}
path3 p=graph(x,y,z,0,1,operator ..);
draw(p,Arrow3);
draw(planeproject(XY*unitsquare3)*p,red,Arrow3);
draw(planeproject(YZ*unitsquare3)*p,green,Arrow3);
draw(planeproject(ZX*unitsquare3)*p,blue,Arrow3);
axes3("$x$","$y$","$z$");
Re: Surface p-V-T d'un corps pur
Posté : lun. 26 avr. 2010, 13:56
par cjorssen
Merci pour ces réponses.
Donc il faut que je me débrouille pour avoir les équations des "frontières" (qui sont des path3). Je crois me souvenir qu'il n'est en revanche pas possible de projeter une surface ?
--
Christophe
Re: Surface p-V-T d'un corps pur
Posté : lun. 26 avr. 2010, 14:05
par GM
Je suis tenté de te dire : trouve l'équation des surfaces... et on verra s'il y a un paramétrage judicieux qui
- permet de n'en dessiner qu'une partie choisie ;
- permet de déterminer les path3 d'intersection à projeter.
Car en matière d'intersection de surfaces 3D, les possibilités sont encore, pour l'instant, limitées et on ne peut répondre qu'au cas par cas.
Un souvenir de thermo de prépa : PV=nRT pour les gaz parfaits ?
Re: Surface p-V-T d'un corps pur
Posté : mar. 27 avr. 2010, 09:57
par cjorssen
Bonjour,
Je suis tenté de te dire : trouve l'équation des surfaces... et on verra s'il y a un paramétrage judicieux.
OK, mais ce n'est pas si simple... En fait, je suis partagé entre ma volonté de faire une "vraie" surface avec des données expérimentales pour un corps pur (mais pour laquelle je manque de données justement) et l'autre solution qui serait de trouver une équation de surface qui colle "qualitativement" comme disent les physiciens.
Un souvenir de thermo de prépa : PV=nRT pour les gaz parfaits ?
Oui, mais justement, le comportement que je souhaite observer ne correspond pas au gaz parfait

--
Christophe
Re: Surface p-V-T d'un corps pur
Posté : mar. 27 avr. 2010, 13:42
par projetmbc
Nul n'est parfait...

J'ai honte de ce mauvais jeu de mots.

Re: Surface p-V-T d'un corps pur
Posté : mar. 27 avr. 2010, 18:14
par cjorssen
Bon, tout ça n'est pas si simple si je veux procéder analytiquement. J'ai fait quelque chose en maple (uniquement pour le domaine liquide, gaz et liquide-gaz) et je ne sais pas si c'est envisageable avec asymptote (il s'agit essentiellement de résoudre numériquement un système d'équations). Si quelqu'un a l'occasion de jeter un coup d'œil, ça serait super.
Tout est là :
http://christophe.jorssen.free.fr/asy/isoT-VdW2.html et
http://christophe.jorssen.free.fr/asy/isoT-VdW2.mws.
Je pourrais évidemment exporter les valeurs numériques trouvées par maple dans asymptote, mais ce serait vraiment pas beau, non

Merci d'avance.
--
Christophe
Re: Surface p-V-T d'un corps pur
Posté : mar. 27 avr. 2010, 19:10
par GM
cjorssen a écrit :Bon, tout ça n'est pas si simple
Surtout pour des personnes qui n'ont plus fait de thermo depuis 21ans.

cjorssen a écrit :je ne sais pas si c'est envisageable avec asymptote (il s'agit essentiellement de résoudre numériquement un système d'équations)
Il n'est pas possible de trouver l'équation de la courbe de coexistence ?
Si on l'avait, il faudrait alors chercher l'intersection avec les isothermes T<Tc, pour tracer les paliers.
Car... je ne crois pas trop à la possibilité de déterminer les points définissant les paliers avec des calculs d'aires.
Je dis cela mais c'est à tester... et pour cela, je te signale cette possibilité :
Peut-on à coup de boucle et de test... déterminer les points utiles correspondants aux surfaces d'aires égales, pour obtenir la courbe de coexistence ? Peut-être, mais est-ce que cela sera rapide : aucune idée, car je n'avais jamais utilisé simpson avant de te le suggérer.
Re: Surface p-V-T d'un corps pur
Posté : mar. 27 avr. 2010, 21:26
par cjorssen
Surtout pour des personnes qui n'ont plus fait de thermo depuis 21ans.
Il n'est jamais trop tard pour s'y remettre ! Et la transdisciplinarité, non mais

Il n'est pas possible de trouver l'équation de la courbe de coexistence ?
Éventuellement, mais ça n'a pas l'air simple analytiquement. "Qualitativement", ça doit être possible en essayant de trouver des équations "qui marchent" à partir du diagramme pT
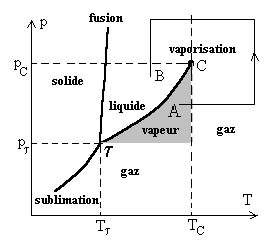
et du diagramme pV
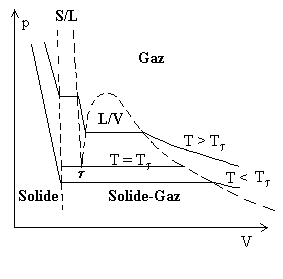
Mais on n'a pas pour autant l'équation de la surface, si je ne m'abuse ?
Merci pour simson, je ne connaissais pas. Mais l'autre problème est que solve ne résout que les systèmes linéaires (si j'ai bien compris). Or, ici, le système à résoudre est non linéaire... snif.
--
Christophe





