Arrow3
Pour toute demande d'aide pour la conception (ou la confirmation d'un code) d'une figure Asymptote, c'est ici.
J'invite ceux qui ont régulièrement des questions à poser à aller dans leur panneau de l'utilisateur pour indiquer dans la signature de leurs messages :
- Nom du système d'exploitation (W7 ou Ubuntu 12.04 ou ...)
- Version d'Asymptote et éditeur utilisé pour les figures Asymptote
- Distribution LaTeX et éditeur utilisé pour les tex.
On va gagner du temps dans les réponses !
Arrow3
Re: Arrow3
merci de fournir une image qui montre une telle flèche.
On doit à OG ceci :
Code : Tout sélectionner
void bracket(picture pic, pair a, pair d, real s,pen p=currentpen)
{
picture opic;
pair ortd=s*(-d.y,d.x);
Draw(opic,(ortd-.5d)--(-0.5d)--0.5d--(.5d+ortd),p+solid);
add(pic,opic,a);
}
arrowbar BeginBra(real size=0, real ratiob=.3)
{
return new bool(picture pic, path g, pen p, margin margin) {
real size=size == 0 ? barsize(p) : size;
bracket(pic,point(g,0),size*dir(g,0)*I,ratiob,p);
return true;
};
}
arrowbar Bra(real size=0, real ratiob=.3)
{
return new bool(picture pic, path g, pen p, margin margin) {
int L=length(g);
real size=size == 0 ? barsize(p) : size;
bracket(pic,point(g,L),size*dir(g,L)*I,-ratiob,p);
return true;
};
}
arrowbar EndBra(real size=0, real ratiob=.3)= Bra;
arrowbar Bras(real size=0,real ratiob=.3)
{
return new bool(picture pic, path g, pen p, margin margin) {
real size=size == 0 ? barsize(p) : size;
BeginBra(size,ratiob)(pic,g,p,margin);
EndBra(size,ratiob)(pic,g,p,margin);
return true;
};
}
arrowbar BeginBra=BeginBra(),
Bra=Bra(),
EndBra=Bra(),
Bras=Bras();

*** Pour masquer/découvrir le code Asymptote qui a permis de créer la figure, il faut cliquer dessus. ;-) ***
- CODE ASYMPTOTE de la figure ci-dessus : Tout sélectionner
- import OG; // pour profiter de "Bras" : extrémités de segment en forme de crochets.
- unitsize(1cm,0);
- draw((0,1)--(5,0),Bra);
- draw((0,.5)--(5,-.5),BeginBra);
- draw((0,0)--(5,-1),EndBra);
- draw((0,-.5)--(5,-1.5),Bras);
- shipout(bbox(5mm,white));
Donc à voir si on peut s'en inspirer... mais il n'a changé que les extrémités donc à voir par quoi doit être remplacé le segment.
Mes configurations (le 24/02/21) :
PC n°1 :Windows 10 - Asymptote(2.82)+MikTeX2.9 - Editeurs : Notepad++, TeXworks, Visual Studio Code.
PC n°2 : Ubuntu 20.04LTS - Asymptote(2.67-?? git) + TexLive2020
Mon serveur : Debian Stretch- Asymptote(2.68-16 git) + TexLive2018
Merci de préciser la votre !
Re: Arrow3
Il devrait être possible de bricoler quelque chose inspiré de cela :
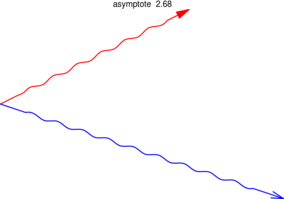
*** Pour masquer/découvrir le code Asymptote qui a permis de créer la figure, il faut cliquer dessus. ;-) ***
- CODE ASYMPTOTE de la figure ci-dessus : Tout sélectionner
- path ondulation(path g, real step=4, real distance=1)
- {
- real len = arclength(g);
- int state = 0;
- guide zig;
- for (real u = 0; u < len; u += step) {
- real t= arctime(g, u);
- pair p = point(g, t);
- pair norm = unit(rotate(90) * dir(g, t));
- if(u<.1*len || u>=.9*len){
- zig = zig -- p;
- }else{
- if (state == 1)
- p = p + distance * norm;
- else if (state == 3)
- p = p - distance * norm;
- zig = zig .. p;
- }
- state = (state + 1) % 4;
- }
- zig = zig .. point(g, length(g));
- return zig;
- }
- // test
- draw(ondulation((0,0) -- (4cm,2cm)),red,Arrow);
- draw(ondulation((0,0) -- (6cm,-2cm)),blue,Arrow(SimpleHead));
Mes configurations (le 24/02/21) :
PC n°1 :Windows 10 - Asymptote(2.82)+MikTeX2.9 - Editeurs : Notepad++, TeXworks, Visual Studio Code.
PC n°2 : Ubuntu 20.04LTS - Asymptote(2.67-?? git) + TexLive2020
Mon serveur : Debian Stretch- Asymptote(2.68-16 git) + TexLive2018
Merci de préciser la votre !
Re: Arrow3
Si c'est une flèche spéciale pour une figure 3D qu'il faut, cela va nettement se compliquer.
Mes configurations (le 24/02/21) :
PC n°1 :Windows 10 - Asymptote(2.82)+MikTeX2.9 - Editeurs : Notepad++, TeXworks, Visual Studio Code.
PC n°2 : Ubuntu 20.04LTS - Asymptote(2.67-?? git) + TexLive2020
Mon serveur : Debian Stretch- Asymptote(2.68-16 git) + TexLive2018
Merci de préciser la votre !
Re: Arrow3
En fait, j'avais préparé une solution pour 2D que je joins ici.
Oui, en effet je cherche (aussi) une solution 3D.
Ce que j'aimerais savoir, au niveau d'Asymptote, c'est si il est possible de modifier une fonction comme Arrow3. Ou si il est possible de programmer une fonction semblable mais en évitant de programmer tous les élements à un niveau élémentaire (comme je le fais).
Je vais étudier les exemples parce que j'ai l'impression qu'ils vont m'apprendre cela.
Pascal

*** Pour masquer/découvrir le code Asymptote qui a permis de créer la figure, il faut cliquer dessus. ;-) ***
- CODE ASYMPTOTE de la figure ci-dessus : Tout sélectionner
- // Visualizing Differential Geometry
- // Draw 1-form
- //
- // Exercise from Tu, An Introduction to Manifolds, Exercises 4.9
- import graph;
- // Size of the drawing. Unit are "big points", a big point is 1/72 inch
- // If you give 2 arguments then this will be breadth and height
- // size(100) yields a quadratic drawing with more than 1 inch (2.54 cm) edge length
- size(400);
- real gridsize = 1.0;
- int igridsize = 1;
- real max=10;
- int imax=10;
- // Length of the bar at the starting and end point of the covector.
- real bl=gridsize*2/10;
- // Debug (*)
- pair DebugPoint=(-2,-2);
- // Debug (+)
- // Labels
- label("-10,-10",(-11,-11),SW,fontsize(6pt));
- label("10,-10",(11,-11),SE,fontsize(6pt));
- label("10,10",(11,11),NE,fontsize(6pt));
- label("-10,10",(-11,11),NW,fontsize(6pt));
- //
- xaxis("$u$", xmin=-max*1.3,xmax=max*1.3,EndArrow);
- yaxis("$v$", ymin=-max*1.3,ymax=max*1.3,EndArrow);
- // Compute covector components as a function of x and y.
- // This is from the textbook Exercise 4.9
- real omegax(real x, real y) {
- return (-y/(x**2+y**2));
- }
- real omegay(real x, real y) {
- return (x/(x**2+y**2));
- }
- pair covectorStartpoint(pair p) {
- return (p.x,p.y);
- }
- pair covectorEndpoint(pair p) {
- return (p.x+omegax(p.x, p.y),p.y+omegay(p.x, p.y));
- }
- real covectorAngleX(pair p) {
- if (omegax(p.x, p.y)==0) {
- if (omegay(p.x, p.y)>0)
- // covector points north
- return pi/2;
- else
- // covector points south
- return 3*pi/2;
- }
- else {
- if (omegax(p.x, p.y) > 0 && omegay(p.x, p.y) > 0) {
- // covector points northeast
- return atan (omegay(p.x, p.y) / omegax(p.x, p.y));
- }
- else if (omegax(p.x, p.y) < 0 && omegay(p.x, p.y) > 0) {
- // covector points northwest
- return (pi + atan (omegay(p.x, p.y) / omegax(p.x, p.y)));
- }
- else if (omegax(p.x, p.y) < 0 && omegay(p.x, p.y) < 0) {
- // covector points southwest
- return (pi + atan (omegay(p.x, p.y) / omegax(p.x, p.y)));
- }
- else if (omegax(p.x, p.y) > 0 && omegay(p.x, p.y) < 0) {
- // covector points southeast
- return (2*pi + atan (omegay(p.x, p.y) / omegax(p.x, p.y)));
- }
- else
- return 0;
- }
- }
- pair covectorHalfBarLengthFromEndpoint(pair p) {
- real covectorTangens;
- real Dx;
- real Dy, DyAbsolute;
- if (omegax(p.x, p.y) != 0) {
- if (omegay(p.x, p.y) != 0) {
- covectorTangens=omegay(p.x, p.y)/omegax(p.x, p.y);
- DyAbsolute=sqrt((covectorTangens^2 * (bl/2)^2) / (1 + covectorTangens^2));
- if (0 < covectorAngleX(p) && covectorAngleX(p) < pi/2) {
- Dy=-DyAbsolute;
- Dx=Dy/covectorTangens;
- } else if (pi/2 < covectorAngleX(p) && covectorAngleX(p) < pi) {
- Dy=-DyAbsolute;
- Dx=Dy/covectorTangens;
- } else if (pi < covectorAngleX(p) && covectorAngleX(p) < 3*pi/2) {
- Dy=DyAbsolute;
- Dx=Dy/covectorTangens;
- } else if (3*pi/2 < covectorAngleX(p) && covectorAngleX(p) < 2*pi) {
- Dy=DyAbsolute;
- Dx=DyAbsolute/covectorTangens;
- }
- // Debug (*)
- //if (p == DebugPoint) {
- //write(p, covectorEndpoint(p), covectorAngleX(p), Dx, Dy, DyAbsolute);
- //}
- // Debug (+)
- return (covectorEndpoint(p).x+Dx,covectorEndpoint(p).y+Dy);
- } else { // horizontal covector
- if (covectorEndpoint(p).x < p.x)
- // covector points left
- return (covectorEndpoint(p).x+bl/2,covectorEndpoint(p).y);
- else
- return (covectorEndpoint(p).x-bl/2,covectorEndpoint(p).y);
- }
- } else { // vertical covector
- if (covectorEndpoint(p).y < p.y)
- // covector points down
- return (covectorEndpoint(p).x,covectorEndpoint(p).y+bl/2);
- else
- return (covectorEndpoint(p).x,covectorEndpoint(p).y-bl/2);
- }
- }
- path arrowLeftpart(pair p) {
- real phi=covectorAngleX(p);
- return (
- (
- (covectorEndpoint(p).x-(bl/2)*sin(phi) + covectorHalfBarLengthFromEndpoint(p).x) / 2,
- (covectorEndpoint(p).y+(bl/2)*cos(phi) + covectorHalfBarLengthFromEndpoint(p).y) / 2
- )--( covectorEndpoint(p) )
- );
- }
- path arrowRightpart(pair p) {
- real phi=covectorAngleX(p);
- return (
- (
- (covectorEndpoint(p).x+(bl/2)*sin(phi) + covectorHalfBarLengthFromEndpoint(p).x) / 2,
- (covectorEndpoint(p).y-(bl/2)*cos(phi) + covectorHalfBarLengthFromEndpoint(p).y) / 2
- )--( covectorEndpoint(p) )
- );
- }
- path covector(pair p) {
- return covectorStartpoint(p)--covectorEndpoint(p);
- }
- real covectorLength(pair p) {
- return sqrt(omegax(p.x, p.y)^2+omegay(p.x, p.y)^2);
- }
- // covector is made of
- // - bar at start point
- // - bar at end point
- // - arrow at end point.
- // The bars are like short segments from level curves showing increase of function value by 1.
- // If the bars are close to each other, the function is steep here.
- // If tha bars are far from each other, the function changes slowly.
- path covectorStartbar(pair p) {
- // Angle of covector with x-axis
- real phi=covectorAngleX(p);
- // draw straight line between start point and end point of the bar
- return ( (p.x-(bl/2)*sin(phi),p.y+(bl/2)*cos(phi))--(p.x+(bl/2)*sin(phi),p.y-(bl/2)*cos(phi)) );
- }
- path covectorEndbar(pair p) {
- // Angle of covector with x-axis
- real phi=covectorAngleX(p);
- // draw straight line between start point and end point of the bar
- return ( (covectorEndpoint(p).x-(bl/2)*sin(phi),covectorEndpoint(p).y+(bl/2)*cos(phi))--(covectorEndpoint(p).x+(bl/2)*sin(phi),covectorEndpoint(p).y-(bl/2)*cos(phi)) );
- }
- // 1-form is a set of covectors defined for any point in the plane
- // it is similar to a vectorfield.
- //
- // We follow a suggestion by Misner, Thorne, Wheeler: Gravity.
- // They do not draw a straight line between start and end point.
- // Instead they draw two bars and a little arrow at the end point.
- //
- // We evaluate the covectors on a grid
- for(int ix=-imax; ix<=imax; ix=ix+igridsize) {
- for (int iy=-imax; iy<=imax; iy=iy+igridsize) {
- if (ix != 0 || iy != 0) {
- pair point=(ix,iy);
- draw(covectorStartbar(point));
- draw(covectorEndbar(point));
- draw(covectorEndpoint(point),red);
- // test
- // draw(covectorHalfBarLengthFromEndpoint(point),green);
- draw(arrowLeftpart(point));
- draw(arrowRightpart(point));
- // Debug (*)
- // if (point == DebugPoint) {
- // write(point, covectorHalfBarLengthFromEndpoint(point));
- // }
- // Debug (+)
- // draw(covector(point));
- }
- }
- }
Re: Arrow3
j'ai du mal à comprendre ce que je vois : si cela ressemble aux flèches qui étaient demandées, je n'avais pas compris ce qui était attendu.
-----------
Pour la question sur Arrow3, je déconseille de modifier une fonction existante.
On peut selon le cas :
- créer une surcharge d'une fonction (c'est à dire créer des fonctions de même nom avec des signatures différentes)
ou alors
- créer une fonction modifiée avec un nom différent.
-----------
La définition de Arrow3(), dans three_arrows.asy est :
Code : Tout sélectionner
arrowbar3 Arrow3(arrowhead3 arrowhead=DefaultHead3,
real size=0, real angle=arrowangle,
filltype filltype=null, position position=EndPoint,
material arrowheadpen=nullpen)
{
return new bool(picture pic, path3 g, material p, margin3 margin,
light light, light arrowheadlight) {
add(pic,arrowhead,size,angle,filltype,position,arrowheadpen,g,p,margin,
light,arrowheadlight);
return false;
};
}DefaultHead3, HookHead3, TeXHead3, DefaultHead2, HookHead2, TeXHead2.
Mes configurations (le 24/02/21) :
PC n°1 :Windows 10 - Asymptote(2.82)+MikTeX2.9 - Editeurs : Notepad++, TeXworks, Visual Studio Code.
PC n°2 : Ubuntu 20.04LTS - Asymptote(2.67-?? git) + TexLive2020
Mon serveur : Debian Stretch- Asymptote(2.68-16 git) + TexLive2018
Merci de préciser la votre !
Re: Arrow3
Re: Arrow3
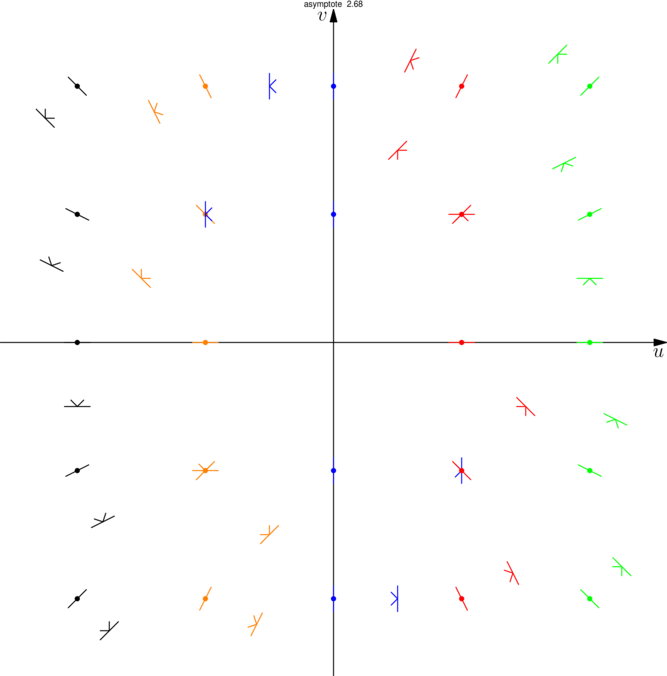
*** Pour masquer/découvrir le code Asymptote qui a permis de créer la figure, il faut cliquer dessus. ;-) ***
- CODE ASYMPTOTE de la figure ci-dessus : Tout sélectionner
- // Visualizing Differential Geometry
- // Draw 1-form
- //
- // Exercise from Tu, An Introduction to Manifolds, Exercises 4.9
- import graph;
- // Size of the drawing. Unit are "big points", a big point is 1/72 inch
- // If you give 2 arguments then this will be breadth and height
- // size(100) yields a quadratic drawing with more than 1 inch (2.54 cm) edge length
- size(400);
- real gridsize = 1.0;
- int igridsize = 1;
- real max=2;
- int imax=2;
- // Length of the bar at the starting and end point of the covector.
- real bl=gridsize*2/10;
- // Debug (*)
- pair DebugPoint=(-2,-2);
- // Debug (+)
- // Labels
- // label("-10,-10",(-11,-11),SW,fontsize(6pt));
- // label("10,-10",(11,-11),SE,fontsize(6pt));
- // label("10,10",(11,11),NE,fontsize(6pt));
- // label("-10,10",(-11,11),NW,fontsize(6pt));
- //
- xaxis("$u$", xmin=-max*1.3,xmax=max*1.3,EndArrow);
- yaxis("$v$", ymin=-max*1.3,ymax=max*1.3,EndArrow);
- // Compute covector components as a function of x and y.
- // This is from the textbook Exercise 4.9
- real omegax(real x, real y) {
- return (-y/(x**2+y**2));
- }
- real omegay(real x, real y) {
- return (x/(x**2+y**2));
- }
- pair covectorStartpoint(pair p) {
- return (p.x,p.y);
- }
- pair covectorEndpoint(pair p) {
- return (p.x+omegax(p.x, p.y),p.y+omegay(p.x, p.y));
- }
- real covectorAngleX(pair p) {
- if (omegax(p.x, p.y)==0) {
- if (omegay(p.x, p.y)>0)
- // covector points north
- return pi/2;
- else
- // covector points south
- return 3*pi/2;
- }
- else {
- if (omegax(p.x, p.y) > 0 && omegay(p.x, p.y) > 0) {
- // covector points northeast
- return atan (omegay(p.x, p.y) / omegax(p.x, p.y));
- }
- else if (omegax(p.x, p.y) < 0 && omegay(p.x, p.y) > 0) {
- // covector points northwest
- return (pi + atan (omegay(p.x, p.y) / omegax(p.x, p.y)));
- }
- else if (omegax(p.x, p.y) < 0 && omegay(p.x, p.y) < 0) {
- // covector points southwest
- return (pi + atan (omegay(p.x, p.y) / omegax(p.x, p.y)));
- }
- else if (omegax(p.x, p.y) > 0 && omegay(p.x, p.y) < 0) {
- // covector points southeast
- return (2*pi + atan (omegay(p.x, p.y) / omegax(p.x, p.y)));
- }
- else
- return 0;
- }
- }
- pair covectorHalfBarLengthFromEndpoint(pair p) {
- real covectorTangens;
- real Dx;
- real Dy, DyAbsolute;
- if (omegax(p.x, p.y) != 0) {
- if (omegay(p.x, p.y) != 0) {
- covectorTangens=omegay(p.x, p.y)/omegax(p.x, p.y);
- DyAbsolute=sqrt((covectorTangens^2 * (bl/2)^2) / (1 + covectorTangens^2));
- if (0 < covectorAngleX(p) && covectorAngleX(p) < pi/2) {
- Dy=-DyAbsolute;
- Dx=Dy/covectorTangens;
- } else if (pi/2 < covectorAngleX(p) && covectorAngleX(p) < pi) {
- Dy=-DyAbsolute;
- Dx=Dy/covectorTangens;
- } else if (pi < covectorAngleX(p) && covectorAngleX(p) < 3*pi/2) {
- Dy=DyAbsolute;
- Dx=Dy/covectorTangens;
- } else if (3*pi/2 < covectorAngleX(p) && covectorAngleX(p) < 2*pi) {
- Dy=DyAbsolute;
- Dx=DyAbsolute/covectorTangens;
- }
- // Debug (*)
- //if (p == DebugPoint) {
- //write(p, covectorEndpoint(p), covectorAngleX(p), Dx, Dy, DyAbsolute);
- //}
- // Debug (+)
- return (covectorEndpoint(p).x+Dx,covectorEndpoint(p).y+Dy);
- } else { // horizontal covector
- if (covectorEndpoint(p).x < p.x)
- // covector points left
- return (covectorEndpoint(p).x+bl/2,covectorEndpoint(p).y);
- else
- return (covectorEndpoint(p).x-bl/2,covectorEndpoint(p).y);
- }
- } else { // vertical covector
- if (covectorEndpoint(p).y < p.y)
- // covector points down
- return (covectorEndpoint(p).x,covectorEndpoint(p).y+bl/2);
- else
- return (covectorEndpoint(p).x,covectorEndpoint(p).y-bl/2);
- }
- }
- path arrowLeftpart(pair p) {
- real phi=covectorAngleX(p);
- return (
- (
- (covectorEndpoint(p).x-(bl/2)*sin(phi) + covectorHalfBarLengthFromEndpoint(p).x) / 2,
- (covectorEndpoint(p).y+(bl/2)*cos(phi) + covectorHalfBarLengthFromEndpoint(p).y) / 2
- )--( covectorEndpoint(p) )
- );
- }
- path arrowRightpart(pair p) {
- real phi=covectorAngleX(p);
- return (
- (
- (covectorEndpoint(p).x+(bl/2)*sin(phi) + covectorHalfBarLengthFromEndpoint(p).x) / 2,
- (covectorEndpoint(p).y-(bl/2)*cos(phi) + covectorHalfBarLengthFromEndpoint(p).y) / 2
- )--( covectorEndpoint(p) )
- );
- }
- path covector(pair p) {
- return covectorStartpoint(p)--covectorEndpoint(p);
- }
- real covectorLength(pair p) {
- return sqrt(omegax(p.x, p.y)^2+omegay(p.x, p.y)^2);
- }
- // covector is made of
- // - bar at start point
- // - bar at end point
- // - arrow at end point.
- // The bars are like short segments from level curves showing increase of function value by 1.
- // If the bars are close to each other, the function is steep here.
- // If tha bars are far from each other, the function changes slowly.
- path covectorStartbar(pair p) {
- // Angle of covector with x-axis
- real phi=covectorAngleX(p);
- // draw straight line between start point and end point of the bar
- return ( (p.x-(bl/2)*sin(phi),p.y+(bl/2)*cos(phi))--(p.x+(bl/2)*sin(phi),p.y-(bl/2)*cos(phi)) );
- }
- path covectorEndbar(pair p) {
- // Angle of covector with x-axis
- real phi=covectorAngleX(p);
- // draw straight line between start point and end point of the bar
- return ( (covectorEndpoint(p).x-(bl/2)*sin(phi),covectorEndpoint(p).y+(bl/2)*cos(phi))--(covectorEndpoint(p).x+(bl/2)*sin(phi),covectorEndpoint(p).y-(bl/2)*cos(phi)) );
- }
- // 1-form is a set of covectors defined for any point in the plane
- // it is similar to a vectorfield.
- //
- // We follow a suggestion by Misner, Thorne, Wheeler: Gravity.
- // They do not draw a straight line between start and end point.
- // Instead they draw two bars and a little arrow at the end point.
- //
- // We evaluate the covectors on a grid
- pen[] couleurs = {blue,red,green,black,orange};
- int n = couleurs.length;
- for(int ix=-imax; ix<=imax; ix=ix+igridsize) {
- for (int iy=-imax; iy<=imax; iy=iy+igridsize) {
- if (ix != 0 || iy != 0) {
- pen coul = couleurs[ix%n];
- pair point=(ix,iy);
- dot(point,3bp+coul);
- draw(covectorStartbar(point),coul);
- draw(covectorEndbar(point),coul);
- draw(covectorEndpoint(point),coul);
- // test
- // draw(covectorHalfBarLengthFromEndpoint(point),green);
- draw(arrowLeftpart(point),coul);
- draw(arrowRightpart(point),coul);
- // Debug (*)
- // if (point == DebugPoint) {
- // write(point, covectorHalfBarLengthFromEndpoint(point));
- // }
- // Debug (+)
- // draw(covector(point));
- }
- }
- }
Mes configurations (le 24/02/21) :
PC n°1 :Windows 10 - Asymptote(2.82)+MikTeX2.9 - Editeurs : Notepad++, TeXworks, Visual Studio Code.
PC n°2 : Ubuntu 20.04LTS - Asymptote(2.67-?? git) + TexLive2020
Mon serveur : Debian Stretch- Asymptote(2.68-16 git) + TexLive2018
Merci de préciser la votre !
Re: Arrow3
Je m'étonne que le code soit aussi long donc j'essaie de comprendre le cahier des charges, sans me laisser influencer par la façon dont le code est proposé.
Je n'ai pas le temps de décortiquer ce qui est proposé et je n'ai d'ailleurs pas le temps de programmer actuellement mais dans l'éventuelle perspective d'une version personnelle du même dessin, je me pose des questions :
La longueur d'une flèche dépend uniquement des coordonnées du point où elle est tracée ?
L'orientation d'une flèche dépend uniquement des coordonnées du point où elle est tracée ?
Autrement dit, est-ce que le covecteur ne dépend que des coordonnées du point où il est tracé ?
Mes configurations (le 24/02/21) :
PC n°1 :Windows 10 - Asymptote(2.82)+MikTeX2.9 - Editeurs : Notepad++, TeXworks, Visual Studio Code.
PC n°2 : Ubuntu 20.04LTS - Asymptote(2.67-?? git) + TexLive2020
Mon serveur : Debian Stretch- Asymptote(2.68-16 git) + TexLive2018
Merci de préciser la votre !
Re: Arrow3
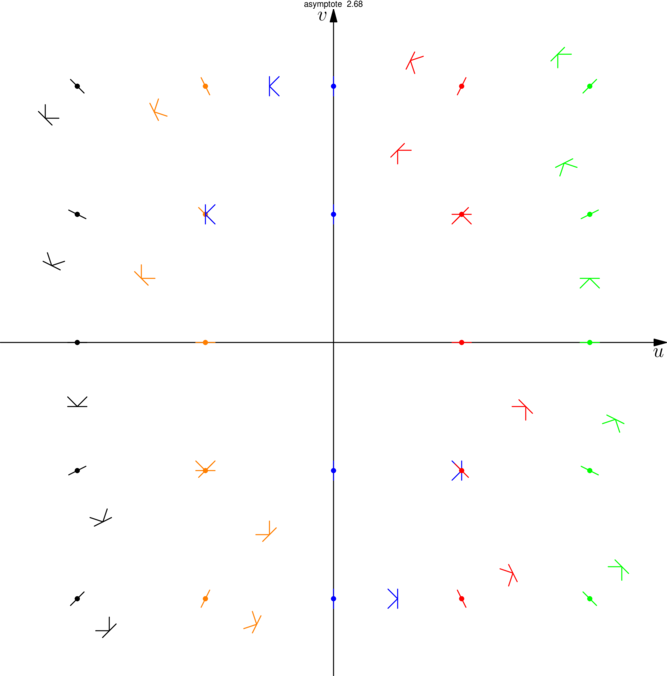
*** Pour masquer/découvrir le code Asymptote qui a permis de créer la figure, il faut cliquer dessus. ;-) ***
- CODE ASYMPTOTE de la figure ci-dessus : Tout sélectionner
- import graph;
- size(400);
- real gridsize=1;
- int igridsize=1;
- real max=2;
- int imax=2;
- pen[] couleurs = {blue,red,green,black,orange};
- int n = couleurs.length;
- path[] covector(pair p, real bl=gridsize*0.15) {
- path tr = (0,bl/2)--(0,-bl/2), // trait que je vais placer aux 2 extrémités
- po = (bl/2,bl/2)--(0,0)--(bl/2,-bl/2); // pointe de flèche
- transform t1 = scale(1/(abs(p))^2),
- t2 = shift(p)*rotate(-90);
- pair A=p, B=shift(p)*rotate(90)*t1*p; // extrémités de la flèche
- // Je retourne un array de 3 path formant la flèche.
- return new path[] {t2*rotate(degrees(p))*tr, // trait 1 au point p
- shift(B-A)*t2*rotate(degrees(p))*tr, // trait 2
- shift(B-A)*t2*rotate(degrees(p))*po // pointe 2
- };
- }
- xaxis("$u$", xmin=-max*1.3,xmax=max*1.3,EndArrow);
- yaxis("$v$", ymin=-max*1.3,ymax=max*1.3,EndArrow);
- for(int ix=-imax; ix<=imax; ix=ix+igridsize) {
- for (int iy=-imax; iy<=imax; iy=iy+igridsize) {
- if (ix != 0 || iy != 0) {
- pen coul = couleurs[ix%n];
- pair pt=(ix,iy);
- dot(pt,3bp+coul);
- draw(covector(pt),coul);
- }
- }
- }
ou s'il faut accéder aux attributs d'un covecteur (points, longueur, angle, ...), traiter le covecteur comme un objet (avec : STRUCT , dans l'esprit de ce qu'à fait Philippe Ivaldi dans l'extension geometry.)
Mes configurations (le 24/02/21) :
PC n°1 :Windows 10 - Asymptote(2.82)+MikTeX2.9 - Editeurs : Notepad++, TeXworks, Visual Studio Code.
PC n°2 : Ubuntu 20.04LTS - Asymptote(2.67-?? git) + TexLive2020
Mon serveur : Debian Stretch- Asymptote(2.68-16 git) + TexLive2018
Merci de préciser la votre !
