Bon je me résigne à vous embêter mais là c'est trop dur pour moi et ce d'autant plus que la doc d'Asymptote est relativement peu épaisse.
Bref voici mon problème; en fait je rebondis sur un sujet précédent mais différent.
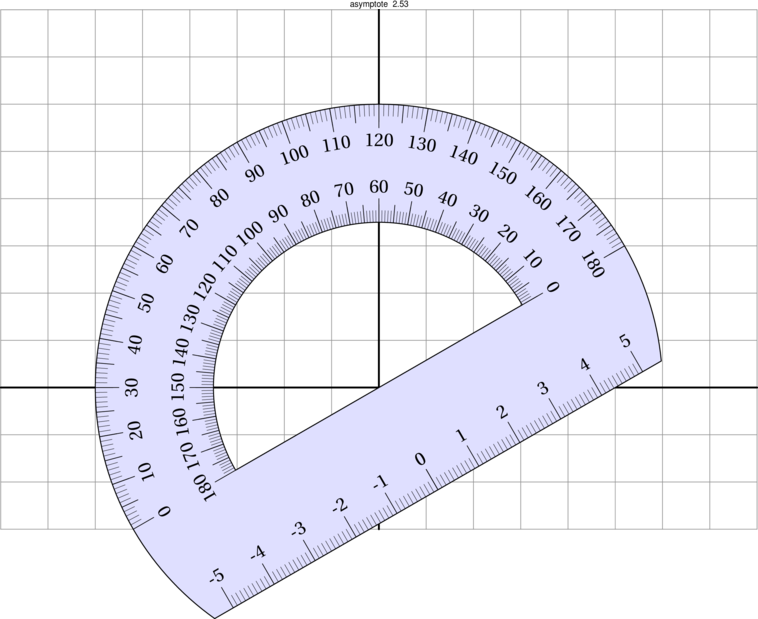
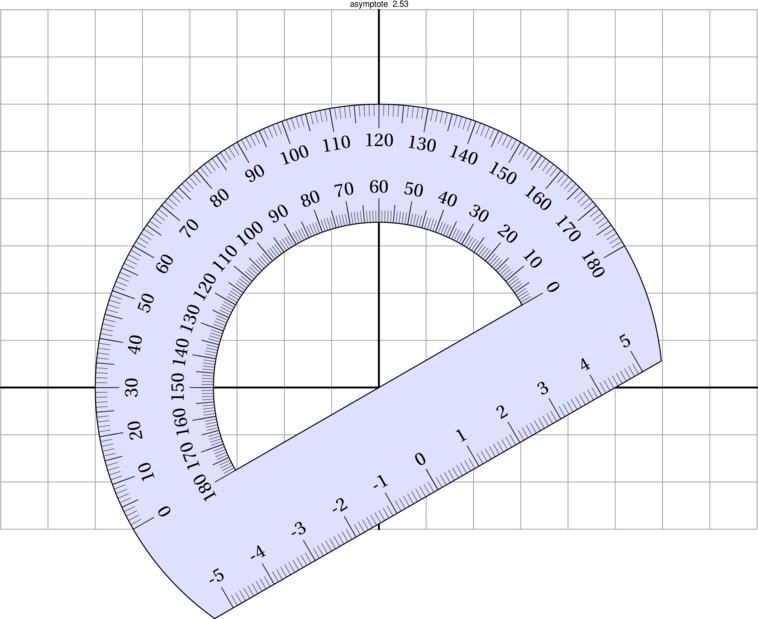
J'ai un joli code pour construire un rapporteur (pas de moi) et je me demande s'il serait possible de le mettre dans une sorte de "void" ou autre routine adéquate afin de l'utiliser sur une feuille dans des positions choisi par moi. Je voudrais essentiellement le placer à un point précis et lui faire subir évidemment une rotation aussi choisie par moi-même.
Voici ce que j'ai fait. Le problème c'est que je ne sais comment lui appliquer une transformation ...
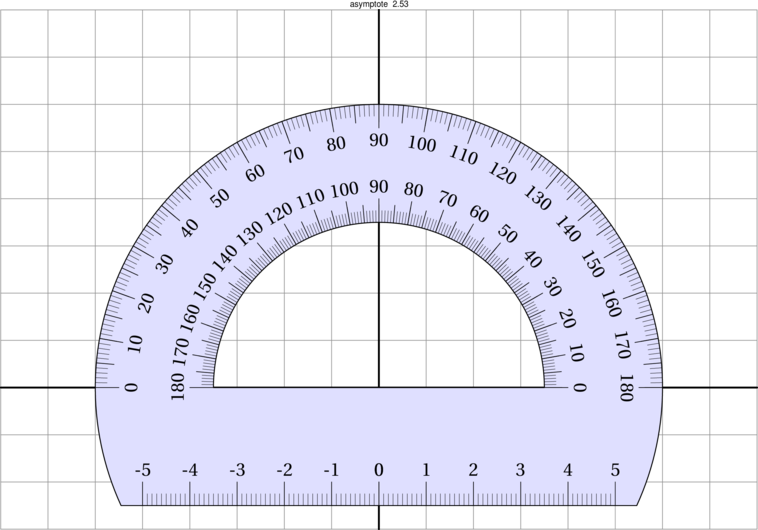
*** Pour masquer/découvrir le code Asymptote qui a permis de créer la figure, il faut cliquer dessus. ;-) ***
- CODE ASYMPTOTE de la figure ci-dessus : Tout sélectionner
- import geometry;
- usepackage("fourier");
- usepackage("amsmath");
- usepackage("siunitx", "locale=DE");
- unitsize(1cm);
- void grille(int xmin, int xmax, int ymin ,int ymax){
- for(int k=ymin; k<=ymax; ++k)
- draw((xmin,k)--(xmax,k),.4bp+gray);
- for(int k=xmin; k<=xmax; ++k)
- draw((k,ymin)--(k,ymax),.4bp+gray);
- draw((xmin,0)--(xmax,0),1pt+black);
- draw((0,ymin)--(0,ymax),1pt+black);
- }
- void rapporteur(real scale=1){
- defaultpen(fontsize(12pt*scale)); // Stylo par défaut
- real r=3.5*scale; // rayon du demi-cercle intérieur : r
- real l=2.5*scale; // largeur du rapporteur : l
- real p=l/10*scale; // largeur des petites graduations
- real g=2p; // largeur des grandes graduations
- point pO=(0,0), pA=(r,0);
- line droiteregle=line(0,-l);
- circle cercleint=circle(pO,r),
- cercleext=circle(pO,r+l);
- point[] R=intersectionpoints(droiteregle,cercleext);
- path chint=arc(cercleint,pA,-pA)--cycle,
- chext=arc(cercleext,R[1],R[0])--cycle;
- filldraw(chint^^chext,paleblue+white+evenodd,0.5bp+black);
- for(int k=0; k<180; ++k){//graduation au 1/10 des 2 cercles
- draw(r*dir(k)--(r+p)*dir(k)^^(r+l-p)*dir(k)--(r+l)*dir(k),0.25bp+black);
- }
- for(int k=0; k<36; ++k){//graduation au 1/5 des 2 cercles
- draw(r*dir(5*k)--(r+0.75g)*dir(5*k)^^(r+l-0.75g)*dir(5*k)--(r+l)*dir(5*k),0.4bp+black);
- }
- for(int k=0; k<=18; ++k) {//graduations de 10 en 10 des 2 cercles
- draw(r*dir(10k)--(r+g)*dir(10k)^^(r+l-g)*dir(10k)--(r+l)*dir(10k),0.4bp+black);
- label(rotate(10k-90)*format("%i",10*k),(r+g)*dir(10k),dir(10k));
- label(rotate(90-10k)*format("%i",10*k),(r+l-g)*dir(180-10k),dir(-10k));
- }
- int xmax=floor(R[1].x);
- for(int x=0; x<10*xmax; ++x){//graduation au 1/10 de la règle
- draw((-x/10,-l)--(-x/10,p-l)^^(x/10,-l)--(x/10,p-l),0.25bp+black);
- }
- for(int x=0; x<=xmax; ++x) {//graduations de la règle
- draw((-x,-l)--(-x,g-l)^^(x,-l)--(x,g-l),0.4bp+black);
- label(format("%i",x),(x,g-l),N);
- label(format("%i",-x),(-x,g-l),N);
- }
- }
- grille(-8,8,-3,8);
- rapporteur();