Loi Normale dans les nouveaux programmes de terminale

[GM]

Rappel de la partie Probabilités/Statistique du nouveau programme de terminale S, pour la rentrée 2012 :

bo_probabililtes_statistique_ts_2012.pdf

(192.54 Kio) Téléchargé 1464 fois

Au programme, notamment :

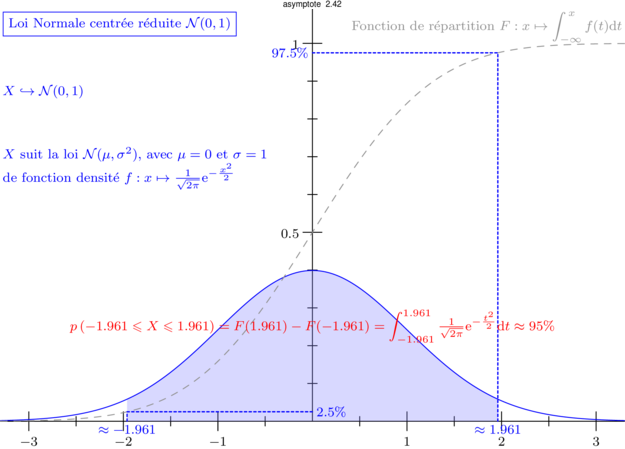
• Loi normale centrée réduite
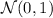
• Loi normale

--------------------------------------

Pour préparer de jolis cours sur le sujet avec le tandem LATEX/ASYMPTOTE, signalons une fonction peut-être méconnue : erf.

Code : Tout sélectionner

// Notons F la fonction de répartition de la loi normale centrée réduite N(0,1)
// dont l'expression F(x) = 1/sqrt(2\pi) * (intégrale de -inf à x de exp(-t^{2}/2) dt)
// peut s'exprimer aussi à l'aide de la fonction d'erreur de Gauss, notée erf.
// erf(x) = 2/sqrt(\pi) * (intégrale de 0 à x de exp(-t^) dt)
// F(x) est la moyenne de 1 et erf(x/sqrt(2))
// ou encore : erf(x)= 2 F(x sqrt(2)) - 1

real F(real x){ return (1+erf(x/sqrt(2)))/2; }

real x=1.96;
write(F(x));            // donne 0.975 (0.97500210485178)
write(F(-x));           // donne 0.025 (0.0249978951482204)
write(F(x)-F(-x));      // donne 0.95  (0.950004209703559)
write(erf(x/sqrt(2)));  // donne 0.95  (0.950004209703559)

real x=2.58;
write(F(x));            // donne 0.995 (0.950004209703559)
write(F(-x));           // donne 0.005 (0.00494001575777064)
write(F(x)-F(-x));      // donne 0.99  (0.990119968484459)
write(erf(x/sqrt(2)));  // donne 0.99  (0.990119968484459)

On vérifie ci-dessus avec Asymptote les deux valeurs de 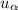à connaitre (spécifiées dans le nouveau programme de TS).

----------

Application : pour obtenir une table numérique de la fonction de répartition associée à la Loi Normale centrée réduite, telle qu'évoquée ici, voilà :

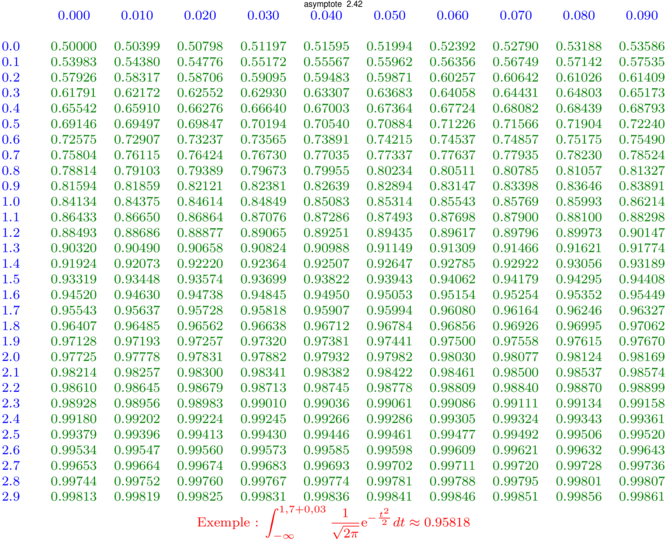
*** Pour masquer/découvrir le code Asymptote qui a permis de créer la figure, il faut cliquer dessus. ;-) ***

CODE ASYMPTOTE de la figure ci-dessus : Tout sélectionner

usepackage("amsmath");
//// Valeurs susceptibles d'êtres modifiées :
real x            = 0;
int  subdivisions = 10,
     nbrlignes    = 30;
 
//// Lignes qui ne devraient pas être à modifier :
defaultpen(fontsize(8pt)+.5green);
real y, pas=.1/subdivisions;
int  nbrvaleurs = nbrlignes*subdivisions;
size(40*subdivisions,10*(nbrlignes+2),IgnoreAspect);
for(int k=0; k<subdivisions; ++k) label(format("%#.3f",k*pas),(k,subdivisions*2),blue);
 
for(int k=0; k<nbrvaleurs; ++k){
  y=(1+erf(x/sqrt(2)))/2;
  label(format("%#.5f",y),(k%subdivisions,k%subdivisions-k));
  if(k/subdivisions==floor(k/subdivisions)) label(format("%#.1f",x),(-1,k%subdivisions-k),blue);
  x=x+pas;
}
label("Exemple : $\displaystyle
       \int_{-\infty}^{1,7+0,03}\frac{1}{\sqrt{2\pi}}\text{e}^{-\frac{t^{2}}{2}}dt\approx 0.95818$",
       truepoint(S),S,red);

-----------------------

NB :

• Les exemples précédents atterriront vraisemblablement dans la sous-galerie des fonctions mathématiques.
• Le sujet est lancé... d'autres messages viendront à la suite de celui-ci sur le même thème de la Loi Normale. Bientôt...

[GM]

Loi Normale centrée réduite : sa fonction densité et la fonction de répartition

*** Pour masquer/découvrir le code Asymptote qui a permis de créer la figure, il faut cliquer dessus. ;-) ***

CODE ASYMPTOTE de la figure ci-dessus : Tout sélectionner

settings.tex="pdflatex";
usepackage("amsmath,amssymb");
 
import geometry;
import graph;
unitsize(2cm,8cm);
 
real  mu=0, sig=1;
real  b=3.3,  a=-b;
real  t=95/100,
      p1=50/100-t/2,
      p2=50/100+t/2;
 
real f(real x){ return 1/(sig*sqrt(2*pi))*exp(-.5*((x-mu)/sig)^2); }
real F(real x){ return (1+erf(x/sqrt(2)))/2; }
 
point[] t1=intersectionpoints(line(0,p1),(path)graph(F,a,b));
point[] t2=intersectionpoints(line(0,p2),(path)graph(F,a,b));
 
fill((graph(f,t1[0].x,t2[0].x,1000))--(t2[0].x,0)--(t1[0].x,0)--cycle,lightblue+opacity(.3));
draw(graph(f,a,b,1000),blue);
draw(graph(F,a,b,1000),dashed+gray);
draw((0,t1[0].y)--t1[0]--(t1[0].x,0),.7bp+blue+linetype("2 2"));
draw((0,t2[0].y)--t2[0]--(t2[0].x,0),.7bp+blue+linetype("2 2"));
 
defaultpen(fontsize(8pt));
label(format("$ %.1f $",p1*100)+"\%",(0,t1[0].y),E,blue);
label(format("$ %.1f $",p2*100)+"\%",(0,t2[0].y),W,blue);
label(format("$\approx %.3f$",t1[0].x),(t1[0].x,0),S,blue);
label(format("$\approx %.3f$",t2[0].x),(t2[0].x,0),S,blue);
 
xaxis(Ticks(NoZero));
yaxis(ymax=1.09,Ticks(NoZero,Step=.5,step=.1));
 
label("$\displaystyle
        p\left("+format("%.3f",t1[0].x)+"\leqslant X\leqslant "+format("%.3f",t2[0].x)+"\right)=
        F("+format("%.3f",t2[0].x)+")-F("+format("%.3f",t1[0].x)+")=
        \int_{"+format("%.3f",t1[0].x)+"}^{"+format("%.3f",t2[0].x)+"}
        \tfrac{1}{\sqrt{2\pi}}\text{e}^{-\frac{t^{2}}{2}}\text{d}t\approx "+
        format("%.1f",100*t)+"\%$",(0,.25),red);
label("Fonction de r\'epartition $\displaystyle F: x\mapsto \int_{-\infty}^{\,x}f(t)\text{d}t$",
      truepoint(NE),SW,gray);
label(minipage("\fbox{Loi Normale centr\'ee r\'eduite $\mathcal{N}(0,1)$}\\[1cm]
                $X\hookrightarrow \mathcal{N}(0,1)$\\[1cm]
                $X$ suit la loi $\mathcal{N}(\mu ,\sigma^2)$, avec $\mu=0$ et $\sigma=1$\\
                de fonction densit\'e $f:x\mapsto \tfrac{1}{\sqrt{2\pi}}\text{e}^{-\frac{x^{2}}{2}}$",
                200pt),truepoint(NW),SE,blue);

[StephaneD]

Juste un gros merci pour la découverte de la fonction erf, la table et ce superbe dessin (c'est exactement ce que je voulais faire, en mieux )!