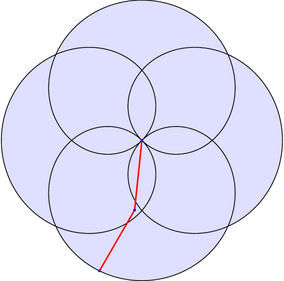
/* Un jongleur de bolas tient une chaîne de même longueur que son bras, 
   tous deux tournant à vitesse constante ; 
   quand son bras fait p tours, sa chaîne en fait q 
   (on prend q>0 si les mouvements sont dans le même sens, et q<0 sinon).
   Alors l'extrémité de sa chaîne décrit une rosace d'indice :
   n = |p-q| / |p+q|

  Dans l'exemple : p=1, q=5 et donc n=2/3.  
*/
import animate;
import graph;

settings.tex="pdflatex";
settings.outformat="pdf";

size(7.5cm,0);

animation A;
real a=2, p=1, q=5, n=abs(p-q)/abs(p+q);
pair pA;
real f(real t) {return a*cos(n*t);}

path g=polargraph(f,0,6pi,600,operator ..)--cycle;
filldraw(g,paleblue+white);
 
for(int k=0; k<360; k+=4) {
  save();
  pA=rotate(k,(0,0))*(a/2,0);
  path brasbolas=(0,0)--pA--pA+rotate(q/p*k,(0,0))*(a/2,0);
  draw(brasbolas,1bp+red);
  dot(brasbolas,2bp+blue);
  A.add();
  restore();
}
A.movie(); // remplacer par la ligne suivante
// label(A.pdf(BBox(1mm,nullpen),delay=500,"controls,loop"));
// pour obtenir une animation dans une seule page d'un pdf.
// controls : pour obtenir les boutons,
// loop : pour que cela tourne en boucle par défaut.

/* Voir explication dans l'exemple précédent.
   On se contente dans celui-ci de changer q=5 en q=-5
   pour obtenir une rosace d'indice n=3/2.
*/
settings.tex="pdflatex";
settings.outformat="pdf";
import graph;
import animation;

size(7.5cm,0);

animation A;
real a=2, p=1, q=-5, n=abs(p-q)/abs(p+q);
pair pA;
real f(real t) {return a*cos(n*t);}

path g=polargraph(f,0,4pi,400,operator ..)--cycle;
filldraw(g,paleblue);

for(int k=0; k<360; k+=4) {
  save();
  pA=rotate(k,(0,0))*(a/2,0);
  path brasbolas=(0,0)--pA--pA+rotate(q/p*k,(0,0))*(a/2,0);
  draw(brasbolas,1bp+red);
  dot(brasbolas,2bp+blue);
  A.add();
  restore();
}
A.movie(); // remplacer par la ligne suivante
// label(A.pdf(BBox(1mm,nullpen),delay=500,"controls,loop"));
// pour obtenir une animation dans une seule page d'un pdf.
// controls : pour obtenir les boutons,
// loop : pour que cela tourne en boucle par défaut.

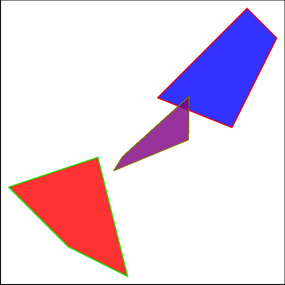
settings.tex="pdflatex";
settings.outformat="pdf";
import geometry;
import animation;

animation A;
size(7.5cm,0);

point A1=(0,0),B1=(2,-1),C1=(1,3),D1=(-2,2),
          A2=(3,5),B2=(6,8),C2=(7,7),D2=(5.5,4);
point barA,barB,barC,barD;        
pen couleur1a=red+opacity(.8),
    couleur2a=blue+opacity(.8),
        couleur3a;
pen couleur1b=green+opacity(.8), 
    couleur2b=red+opacity(.8),
        couleur3b;
path quadri1=A1--B1--C1--D1--cycle,
     quadri2=A2--B2--C2--D2--cycle;

filldraw(quadri1,couleur1a,couleur1b);
filldraw(quadri2,couleur2a,couleur2b);

for (real k=0; k <=1; k+=0.01) {
  save();
  barA=(1-k)*A1+k*A2;
  barB=(1-k)*B1+k*B2;
  barC=(1-k)*C1+k*C2;
  barD=(1-k)*D1+k*D2;
  couleur3a=(1-k)*couleur1a+k*couleur2a;
  couleur3b=(1-k)*couleur1b+k*couleur2b;
  filldraw(barA--barB--barC--barD--cycle,
           couleur3a+opacity(.8),couleur3b+opacity(.8));
  picture pic;
  add(pic,bbox(2mm));
  A.add(pic);
  restore();
}
for (real m=0; m <=1; m+=0.01) {
  save();
  real k=1-m;
  barA=(1-k)*A1+k*A2;
  barB=(1-k)*B1+k*B2;
  barC=(1-k)*C1+k*C2;
  barD=(1-k)*D1+k*D2;
  couleur3a=(1-k)*couleur1a+k*couleur2a;
  couleur3b=(1-k)*couleur1b+k*couleur2b;
  filldraw(barA--barB--barC--barD--cycle,
           couleur3a+opacity(.8),couleur3b+opacity(.8));
  picture pic;
  add(pic,bbox(2mm));
  A.add(pic);
  restore();
}
A.movie(); // remplacer par la ligne suivante
// label(A.pdf(BBox(1mm,nullpen),delay=500,"controls,loop"));
// pour obtenir une animation dans une seule page d'un pdf.
// controls : pour obtenir les boutons,
// loop : pour que cela tourne en boucle par défaut.

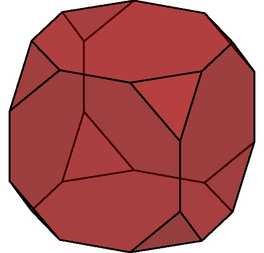
import polyhedron_js;
import animate;

settings.render=0;
settings.tex="pdflatex";
settings.outformat="pdf";

size(7cm,0);
currentprojection=orthographic(1,0.5,0.5);
currentlight=(1,1,2);

animation A;
polyhedron[] parr;
pen[] coul={.7red};

for (int k=0; k<360; k+=3) {
  save();
  transform3 T=rotate(-degrees(2pi*k/360),Z);
  parr[0]=T*truncCube;
  filldraw(parr,coul,op=0.5);
  A.add();
  restore();
}
A.movie(); // remplacer par la ligne suivante
// label(A.pdf(BBox(1mm,nullpen),delay=500,"controls,loop"));
// pour obtenir une animation dans une seule page d'un pdf.
// controls : pour obtenir les boutons,
// loop : pour que cela tourne en boucle par défaut.

/* La néphroïde est une épicycloïde à deux rebroussements. 
   (obtenu notamment en faisant rouler un cercle de rayon a/2
    à l'extérieur d'un cercle de rayon a).
*/
import geometry;
import animate;

settings.tex="pdflatex";
settings.outformat="pdf";

size(7.5cm,0);

animation A;
real a=2;
pair pM, pC, pN;
path nephroide;

draw(scale(a)*unitcircle);

for(int k=0; k<360; k+=3) {
  save();
  pM=rotate(k,(0,0))*(a,0);
  pC=1.5*pM;
  pN=rotate(2*k,pC)*pM;
  nephroide=nephroide..pN;
  draw(shift(pC)*scale(a/2)*unitcircle);
  draw(nephroide,1bp+red);
  draw(pN--pC,1bp+paleblue);dot(pN--pC,3bp+blue);
  A.add();
  restore();
}
A.movie(); // remplacer par la ligne suivante
// label(A.pdf(BBox(1mm,nullpen),delay=500,"controls,loop"));
// pour obtenir une animation dans une seule page d'un pdf.
// controls : pour obtenir les boutons,
// loop : pour que cela tourne en boucle par défaut.

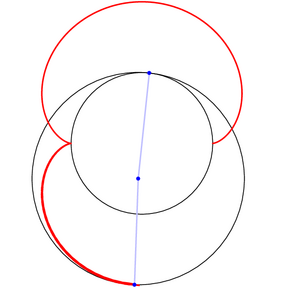
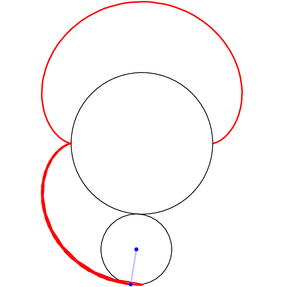
/* La néphroïde est aussi une péricycloïde.
   (On peut l'obtenir aussi en faisant rouler un cercle de rayon 3a/2
    sur un cercle "intérieur" de rayon a).
*/
import geometry;
import animate;

settings.tex="pdflatex";
settings.outformat="pdf";

size(7.5cm,0);

animation A;
real a=2;
pair pM, pC, pN;
path nephroide;

draw(scale(a)*unitcircle);

for(int k=0; k<1080; k+=4) {
  save();
  pM=rotate(k,(0,0))*(a,0);
  pC=-0.5*pM;
  pN=rotate(-2*k/3,pC)*pM;
  nephroide=nephroide..pN;
  draw(shift(pC)*scale(3*a/2)*unitcircle);
  draw(nephroide,1bp+red);
  draw(pN--pC--pM,1bp+paleblue);dot(pN--pC--pM,3bp+blue);
  A.add();
  restore();
}
A.movie(); // remplacer par la ligne suivante
// label(A.pdf(BBox(1mm,nullpen),delay=500,"controls,loop"));
// pour obtenir une animation dans une seule page d'un pdf.
// controls : pour obtenir les boutons,
// loop : pour que cela tourne en boucle par défaut.

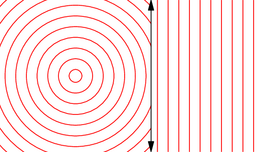
import geometry;
import animate;

settings.tex="pdflatex";
settings.outformat="pdf";

unitsize(2cm);

animation A;
int n=10;

for(int k=0; k<n; ++k){
  for(int i=0; i<10; ++i) draw(scale(sqrt(2)*((k/n)+i)/10)*unitcircle,red);
  clip(shift(-1,-1)*scale(2)*unitsquare);
  for(int i=0; i<10; ++i) draw(shift(sqrt(2)*((k/n)+i)/10,0)*((1,-1)--(1,1)),red);
  draw((1,-1)--(1,1),Arrows);
  A.add();
  erase();
}
A.movie(); // remplacer par la ligne suivante
// label(A.pdf(BBox(1mm,nullpen),delay=500,"controls,loop"));
// pour obtenir une animation dans une seule page d'un pdf.
// controls : pour obtenir les boutons,
// loop : pour que cela tourne en boucle par défaut.

// Cardioïde comme enveloppe de cercles
import geometry;
import animate;
settings.tex="pdflatex";
settings.outformat="pdf";

unitsize(2cm);

animation A;
int n=72;

fill(unitcircle,palered);
for(int k=0; k<n; ++k){
  pair pM=dir(90+k/n*360);
  draw(circle((0,1),pM),gray);
  save();
  dot(pM,1bp+red);
  A.add();
  restore();
}
A.movie(); // remplacer par la ligne suivante
// label(A.pdf(BBox(1mm,nullpen),delay=500,"controls,loop"));
// pour obtenir une animation dans une seule page d'un pdf.
// controls : pour obtenir les boutons,
// loop : pour que cela tourne en boucle par défaut.

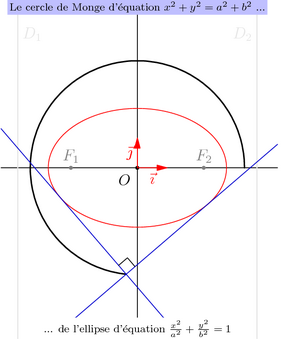
/* La courbe orthoptique d'une courbe est le lieu des points
   d'où l'on "voit" la courbe sous un angle droit.
   L'orthoptique d'une conique à centre d'excentricité inférieure à rac(2)
   est un cercle appelé cercle orthoptique ou cercle de Monge.
   Pour l'ellipse d'équation x^2/a^2+y^2/b^2=1,
   le cercle de Monge a pour équation :  x^2+y^2 = a^2+b^2
*/   
import geometry;
import animate;
settings.tex="pdflatex";
settings.outformat="pdf";

size(7.5cm,0);

animation Anim;
real a=3, b=2, r=sqrt(a^2+b^2);
pair pM;
path cerclemonge;

show(currentcoordsys);

ellipse Ell = ellipse((0,0), a, b);
draw(Ell,red);

draw(Label("$D_1$",align=E),Ell.D1,.8bp+lightgray);
draw(Label("$D_2$",align=W),Ell.D2,.8bp+lightgray);
dot("$F_1$",Ell.F1,N,3bp+gray);
dot("$F_2$",Ell.F2,N,3bp+gray);

for(int k=0; k<360; k+=4) {
  pM=rotate(k,(0,0))*(r,0);
  cerclemonge=cerclemonge..pM;
  save();
  draw(cerclemonge,1bp+black);
  line[] tgs=tangents(Ell, pM);
  draw(tgs,0.8*blue);
  perpendicularmark(tgs[0],tgs[1]);
  addMargins(1cm,1cm);
  label("\scriptsize Le cercle de Monge d'\'equation $x^2+y^2=a^2+b^2$ ...",
        (0,1.5*r),Fill(paleblue));
  label("\scriptsize ... de l'ellipse d'\'equation $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$",
        (0,-1.5*r),Fill(white));
  Anim.add();
  restore();
}
Anim.movie(); // remplacer par la ligne suivante
// label(A.pdf(BBox(1mm,nullpen),delay=500,"controls,loop"));
// pour obtenir une animation dans une seule page d'un pdf.
// controls : pour obtenir les boutons,
// loop : pour que cela tourne en boucle par défaut.

/* L'astroïde est une hypocycloïde à quatre rebroussements 
   (lieu décrit par un point choisi d'un cercle de rayon a/4 (ou 3a/4)
   roulant à l'intérieur d'un autre cercle de rayon a). 
*/
import geometry;
import animate;
settings.tex="pdflatex";
settings.outformat="pdf";

size(7.5cm,0);

animation A;
real a=3;
pair pM, pC, pN;
path astroide;

draw(scale(a)*unitcircle);

for(int k=0; k<360; k+=2) {
  save();
  pM=rotate(k,(0,0))*(a,0);
  pC=3/4*pM;
  pN=rotate(-4*k,pC)*pM;
  astroide=astroide..pN;
  draw(circle(pC,a/4));
  draw(astroide,1bp+red);
  draw((0,0)--pC--pN,1bp+paleblue);
  dot((0,0)--pC--pN,3bp+blue);
  A.add();
  restore();
}
A.movie(); // remplacer par la ligne suivante
// label(A.pdf(BBox(1mm,nullpen),delay=500,"controls,loop"));
// pour obtenir une animation dans une seule page d'un pdf.
// controls : pour obtenir les boutons,
// loop : pour que cela tourne en boucle par défaut.

// Un ancien exemple de Ph. Ivaldi

import animate;
settings.tex="pdflatex";
settings.outformat="pdf";

size(7cm); 
animation A;

void koch(pair A, pair B, int n) { 
          pair C; 
          C=rotate(120, point(A--B,1/3))*A; 
          if (n>0) { 
             koch(A,point(A--B,1/3),n-1); 
             koch(point(A--B,1/3),C,n-1); 
             koch(C,point(A--B,2/3),n-1); 
             koch(point(A--B,2/3),B,n-1); 
          } 
          else draw(A--point(A--B,1/3)--C--point(A--B,2/3)--B);
} 
 
pair z0=(1,0); 
pair z1=rotate(120)*z0; 
pair z2=rotate(120)*z1; 
real pmax=4;
for (int p=0; p<=pmax; p+=1) {
  save();
  koch(z0,z1,p); 
  koch(z1,z2,p); 
  koch(z2,z0,p);
  A.add();
  erase();
}
A.movie(); // remplacer par la ligne suivante
// label(A.pdf(BBox(1mm,nullpen),delay=500,"controls,loop"));
// pour obtenir une animation dans une seule page d'un pdf.
// controls : pour obtenir les boutons,
// loop : pour que cela tourne en boucle par défaut.

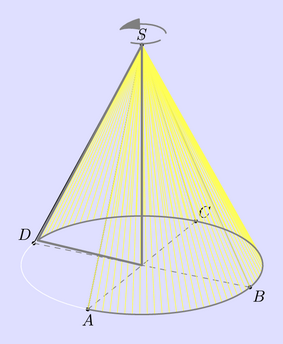
// ----- Génération d'un cône -----

import three;
import animate;
settings.tex="pdflatex";
settings.outformat="pdf";
settings.render=0;

size(7.5cm,0);
currentprojection=orthographic(1,0.5,0.5);

real h=2, abscurv;
triple pO=(0,0,0), pS =(0,0,2h), pA=(h,0,0),
       pB=(0,h,0), pC=(-h,0,0), pD=(0,-h,0);
path3  basegras,base=pA..pB..pC..pD..pA, generatrice;

animation A;
dot("$S$",pS,align=N);
dot("$A$",pA,align=S); dot("$B$",pB,align=SE);
dot("$C$",pC,align=NE); dot("$D$",pD,align=NW);
draw(pA--pS--pC^^pB--pS--pD);
draw(pA--pC^^pB--pD,dashed+grey);
draw(pO--(0,0,2.1*h),dashdotted+grey);
draw(base,grey+white);
draw((0.2h,0,2.1h)..(0,0.2h,2.1h)..(-0.2h,0,2.1h)..(0,-0.2h,2.1h),
      longdashed+1bp+grey,Arrow3());

for(real i=0; i<=1; i+=.01) {
  abscurv = length(base)*i;
  generatrice=pS--point(base,abscurv);
  draw(generatrice,grey+yellow);
  save();
  draw(pO--generatrice--cycle,1.5bp+grey);
  basegras=basegras..point(base,abscurv);
  draw(basegras,1bp+grey);
  picture pic;
  add(pic,bbox(5mm,Fill(paleblue+white)));
  A.add(pic);
  restore();
}
A.movie(); // remplacer par la ligne suivante
// label(A.pdf(BBox(1mm,nullpen),delay=500,"controls,loop"));
// pour obtenir une animation dans une seule page d'un pdf.
// controls : pour obtenir les boutons,
// loop : pour que cela tourne en boucle par défaut.

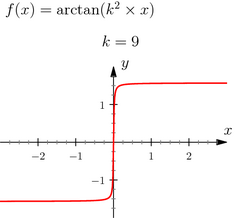
import gm;
import animate;
settings.tex="pdflatex";
settings.outformat="pdf";

unitsize(1cm);

animation A;
pen[] stylo={blue,green,red};
real  xmin=-3, xmax=3, ymin=-2, ymax=2;
int[] k={1,2,3,4,5,6,7,8,9,10,11,12};
real  f(real x,real k) {return atan(k^2*x);}

A = animpdf_famille_fonctions(f,xmin,xmax,ymin,ymax,k,stylo);
for(int i=0; i<A.pictures.length; ++i)
label(A.pictures[i],"$f(x)=\arctan(k^2\times x)$",(xmin,ymax+1.5),E);

A.movie(); // remplacer par la ligne suivante
// label(A.pdf(BBox(1mm,nullpen),delay=500,"controls,loop"));
// pour obtenir une animation dans une seule page d'un pdf.
// controls : pour obtenir les boutons,
// loop : pour que cela tourne en boucle par défaut.