// Présentation des applications affines (de base)
// dans Asymptote.

size(8cm,10cm,IgnoreAspect);
usepackage("fourier","upright");

label(minipage("\small
                Un point $(x;y)$ est transform\'e par l'application
                affine $t=(t.x,t.y,t.xx,t.xy,t.yx,t.yy)$ en le point $(x';y')$
                tel que :\\
                $\left\{\begin{array}{l}
                        x'=t.x+t.xx\times x+t.xy\times y \\
                        y'=t.y+t.yx\times x+t.yy\times y \\
                        \end{array}\right.$",8cm),(0,4),E);

label("\bf Applications affines (pr\'ed\'efinies)",(0,1),E);
string[] t={"identity()",
            "shift(pair z)",
            "shift(real x, real, y)",
            "xscale(real x)",
            "yscale(real y)",
            "scale(real s)",
            "scale(real x, real y)",
            "slant(real s)",
            "rotate(real angle, pair z=(0,0))",
            "reflect(pair a, pair b)"
            };

for(int y=0; y<t.length; ++y) dot(t[y],(0,-y),3E);

label("\bf Libre \`a vous d'en d\'efinir d'autres ! ;-)",(0,-10),E);

// Présentation des applications affines
// ajoutées par l'extension geometry.

size(8.5cm,12cm,IgnoreAspect);
usepackage("fourier","upright");

label(minipage("\small\it
                Rappelons que l'extension geometry de Ph.Ivaldi
                introduit la possibilit\'e de travailler dans plusieurs rep\`eres
                et de nouveaux types d'objets (point, segment, line, triangle, arc, ...)
                auxquels peuvent s'appliquer 
                les applications pr\'ec\'edentes.",8.5cm),(0,4),E);

label("\bf Applications affines ajout\'ees par geometry.asy",(0,1),E);
string[] t={"scale(real k, point M)",
            "projection(point A, point B)",
            "scale({\footnotesize real k,point A,point B,point C,point D,bool safe=false})",
            "xscale(real k, point M)",
            "yscale(real k, point M)",
            "scaleO(real x)",
            "xscaleO(real x)",
            "rotateO(real angle)",
            "reflect(line l)",
            "reflect(line l1, line l2, bool safe=false)",
            "scale(real k, line l1, line l2, bool safe=false)",
            "projection(line l)",
            "projection(line l1, line l2, bool safe=false)",
            "vprojection(line l, bool safe=false)",
            "hprojection(line l, bool safe=false)"
            };
for(int y=0; y<t.length; ++y) dot(t[y],(0,-y),3E);


label("\bf Libre \`a vous d'en d\'efinir d'autres ! ;-)",(0,-15),E);

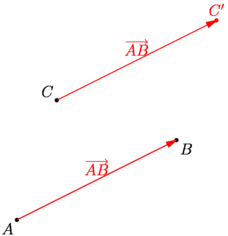
/* Image d'un point par translation */

size(6cm,0);

// Placement de 3 points donnés
pair A=(0,0),B=(4,2),C=(1,3);
dot("$A$",A,SW);
dot("$B$",B,SE);
dot("$C$",C,NW);

// Définition de l'image C' de C
// par la translation de vecteur AB
pair imC=C+(B-A);

// Construction de C'
dot("$C'$",imC,N,red);

// Tracé des vecteurs
draw(Label("$\overrightarrow{AB}$"),A--B,N,red,Arrow);
draw(Label("$\overrightarrow{AB}$"),C--imC,N,red,Arrow);

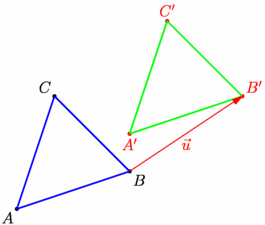
/* Image d'un triangle par translation */

size(7cm,0);

// Placement de 3 points donnés
pair A=(0,0),B=(3,1),C=(1,3);
dot("$A$",A,SW);
dot("$B$",B,SE);
dot("$C$",C,NW);

// Définition de la translation t de vecteur u(3;2)
transform t=shift(3,2);

// Construction des images de A, B, C par t
dot("$A'$",t*A,S,red);
dot("$B'$",t*B,NE,red);
dot("$C'$",t*C,N,red);

// Tracé des triangles ABC et A'B'C'
draw(A--B--C--cycle,1bp+blue);
draw(t*A--t*B--t*C--cycle,1bp+green);

// Tracé du vecteur de la tranlation
draw(Label("$\vec{u}$"),B--t*B,S,red,Arrow);

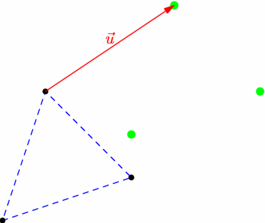
/* Image d'un triangle par translation */

size(7cm,0);

// Placement de 3 points donnés
pair A=(0,0),B=(3,1),C=(1,3);

// Définition du triangle et son tracé
path tr=A--B--C--cycle;
draw(tr,dashed+blue);

// Définition de la translation t de vecteur u(3;2)
transform t=shift(3,2);

// Placement des sommets de tr et du triangle image
dot(tr,linewidth(4bp));
dot(t*tr,green+6bp);

// Tracé du vecteur de la tranlation
draw(Label("$\vec{u}$"),C--t*C,N,red,Arrow);

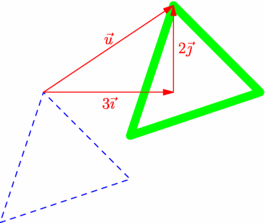
/* Image d'un triangle par translation */

size(7cm,0);

// Placement de 3 points donnés
pair A=(0,0),B=(3,1),C=(1,3);

// Définition du triangle et son tracé
path tr=A--B--C--cycle;
draw(tr,dashed+blue);

// Définition de la translation t de vecteur u(3;2)
transform t=shift(3,2);

// Traxé du triangle image
draw(t*tr,green+6bp);

// Tracé du vecteur de la tranlation
draw(Label("$\vec{u}$"),C--t*C,N,red,Arrow);
draw(Label("$3\vec{\imath}$"),C--C+(3,0),S,red,Arrow);
draw(Label("$2\vec{\jmath}$"),C+(3,0)--C+(3,2),E,red,Arrow);

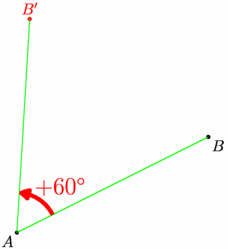
/* Image d'un point par rotation */

size(6cm,0);
import markers;

// Placement de 2 points donnés
pair pA=(0,0),pB=(4,2);
dot("$A$",pA,SW);
dot("$B$",pB,SE);

// Définition de l'image B' de B
// par la rotation de centre A et d'angle 60°
pair imB=rotate(60,pA)*pB;
// Construction de B'
dot("$B'$",imB,N,red);
draw(pB--pA--imB,green);

markangle(scale(1.5)*"$+60^\circ$",radius=30,
           pB,pA,imB,ArcArrow(2mm),1mm+red);

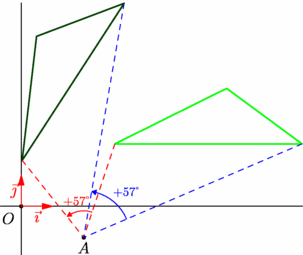
/* Image d'un triangle par rotation
   (avec les types et fonctions de l'extension geometry
*/
size(8cm,0);
import geometry;
import markers;
import babel; babel("frenchb"); // pour \degrees

show(currentcoordsys);
triangle tri=triangleabc(3,4,6,(3,2));
// tri=triangleabc(a=3,b=4,c=6,angle=0,A=(3,2));
// tri est un triangle ABC direct, tel que :
//                     A=(3,2), 
//                     (vec(i),vec(AB))=0,
//                     a=BC=3,b=AC=4,c=AB=6
point Om=(2,-1);
transform r=rotate(57,Om);
dot("$A$",Om,S);
draw(tri,1bp+green);
draw(r*tri,1bp+darkgreen);
draw(tri.A--Om--r*tri.A,dashed+red); // 
draw(tri.B--Om--r*tri.B,dashed+blue);
// r*tri est l'image de tri par la rotation r
// tri.A, tri.B et tri.C désignent les sommets de tri
markangle(scale(.8)*"$+57\degres$",radius=20,
           tri.A,Om,r*tri.A,ArcArrow(3bp),.5bp+red);
markangle(scale(.8)*"$+57\degres$",radius=35,
           tri.B,Om,r*tri.B,ArcArrow(3bp),.5bp+blue);              

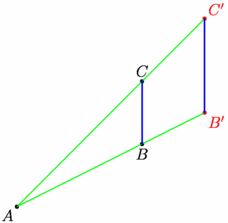
/* Image d'un point par homothétie */

size(6cm,0);
// Définition d'une fonction renvoyant
// l'image d'un point M par une homothétie
pair ImageParHom(pair M, real k, pair Centre) {
  return shift(k*(M-Centre))*Centre;
}
// Placement de 3 points donnés
pair pA=(0,0),pB=(2,1),pC=(2,2);
dot("$A$",pA,SW);
dot("$B$",pB,S);
dot("$C$",pC,N);

// Définition des image B' et C' de B et C
// par l'homothétie de centre A et de rapport 1,5
pair imB=ImageParHom(pB,1.5,pA),
        imC=ImageParHom(pC,1.5,pA);
// Construction de B' et C', des segments
dot("$B'$",imB,SE,red);dot("$C'$",imC,NE,red);
draw(imB--pA--imC,green);
draw(pB--pC^^imB--imC,1bp+blue);

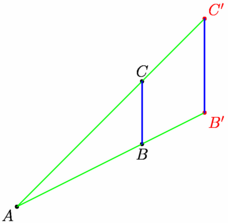
/* L'exemple précédent amélioré...
   cette fois, on définit une transformation homothétie
*/
size(6cm,0);
// Définition d'une tranformation homothétie
transform Homothetie(real k, pair centre)
{
  return shift(centre)*scale(k)*shift(-centre);
}
// Placement de 3 points donnés
pair pA=(0,0),pB=(2,1),pC=(2,2);
dot("$A$",pA,SW);
dot("$B$",pB,S);
dot("$C$",pC,N);
// Définition de h, l'homothétie de centre pA et de rapport 1.5
transform h=Homothetie(1.5,pA);
// Définition des image B' et C' de B et C par h
pair imB=h*pB, imC=h*pC;
// Construction de B' et C', des segments
dot("$B'$",imB,SE,red);dot("$C'$",imC,NE,red);
draw(imB--pA--imC,green);
draw(pB--pC^^imB--imC,1bp+blue);

// import geometry_dev; // extension devenue l'extension geometry officielle
import geometry;        // le 12/05/09, dans la version 1.71 d'asymptote. :-))

size(6cm,0);
// Placement de 3 points donnés
pair pA=(0,0),pB=(2,1),pC=(2,2);
dot("$A$",pA,SW);
dot("$B$",pB,S);
dot("$C$",pC,N);
// Définition de h, l'homothétie de centre pA et de rapport 1.5
transform h=scale(1.5,pA);
// Définition des image B' et C' de B et C par h
pair imB=h*pB, imC=h*pC;
// Construction de B' et C', des segments
dot("$B'$",imB,SE,red);dot("$C'$",imC,NE,red);
draw(imB--pA--imC,green);
draw(pB--pC^^imB--imC,1bp+blue);

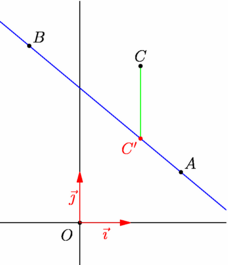
/* Image d'un point par projection "horizontale"
   en utilisant la fonction hprojection de l'extension geometry
   Syntaxe :
                transform hprojection(line l, bool safe=false)
*/
// import geometry_dev; // extension devenue l'extension geometry officielle
import geometry;        // le 12/05/09, dans la version 1.71 d'asymptote. :-))

size(6cm,0);
show(currentcoordsys);

// Définition de 3 points donnés
point A=(2,1),B=(-1,3.5),C=(1.2,3.1);
// et de l'image C' de C par projection sur (AB)
// parallèlement à l'axe des abscisses.
pair imC=hprojection(line(A,B))*C;

// Constructions
draw(line(A,B),blue);
draw(segment(C,imC),green);
dot("$A$",A,NE); dot("$B$",B,NE);
dot("$C$",C,N); dot("$C'$",imC,SW,red);

addMargins(1cm,1cm);

/* Image d'un point par projection "verticale"
   en utilisant la fonction vprojection de l'extension geometry
   Syntaxe :
                transform vprojection(line l, bool safe=false)
*/
// import geometry_dev; // extension devenue l'extension geometry officielle
import geometry;        // le 12/05/09, dans la version 1.71 d'asymptote. :-))

size(6cm,0);
show(currentcoordsys);

// Définition de 3 points donnés
point A=(2,1),B=(-1,3.5),C=(1.2,3.1);
// et de l'image C' de C par projection sur (AB)
// parallèlement à l'axe des abscisses.
pair imC=vprojection(line(A,B))*C;

// Constructions
draw(line(A,B),blue);
draw(segment(C,imC),green);
dot("$A$",A,NE); dot("$B$",B,NE);
dot("$C$",C,N); dot("$C'$",imC,SW,red);

addMargins(1cm,1cm);

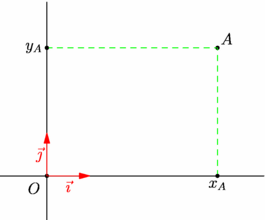
/* Projection d'un point sur les axes du repère 
   avec l'extension geometry_dev en utilisant :
   les fonctions de projection horizontale et verticale
        transform vprojection(line l, bool safe=false)
        transform vprojection(line l, bool safe=false)
   les constantes (de type line) prédéfinies :
            line Ox
        line Oy
*/
import geometry;

size(7cm,0);
show(currentcoordsys);

// Définition d'un point...
point A=(4,3);
// ... et de ses projetés sur les axes.
point xA=vprojection(Ox)*A,
      yA=hprojection(Oy)*A;
/* ATTENTION ! Cf. exemple suivant,
   pour une méthode plus courte.
*/

// Constructions
dot("$A$",A,NE);
draw(xA--A--yA,dashed+green);
dot("$x_A$",xA,S);
dot("$y_A$",yA,W);

addMargins(1cm,1cm);

/* La même construction que précédemment
   avec une autre méthode... plus rapide !
*/
// import geometry_dev; // extension devenue l'extension geometry officielle
import geometry;        // le 12/05/09, dans la version 1.71 d'asymptote. :-))

size(7cm,0);
show(currentcoordsys);

// Définition d'un point...
point A=(4,3);
// ... et de ses projetés sur les axes.
// en utilisant les coordonnées.
point xA=(A.x,0),
      yA=(0,A.y);

// Constructions
dot("$A$",A,NE);
draw(xA--A--yA,dashed+green);
dot("$x_A$",xA,S);
dot("$y_A$",yA,W);

addMargins(1cm,1cm);

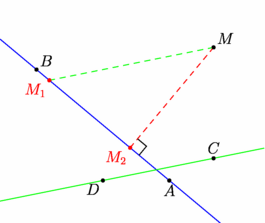
/* Projections sur une droite définie par deux points A et B
a) orthogonalement
    transform projection(point A, point B)
b) parallèlement à une autre droite définie par deux points C et D
    transform projection(point A, point B, point C, point D, bool safe=false)
*/
// import geometry_dev; // extension devenue l'extension geometry officielle
import geometry;        // le 12/05/09, dans la version 1.71 d'asymptote. :-))

size(7cm,0);

// Définition de 5 points donnés
point A=(2,1),B=(-1,3.5),C=(3,1.5),D=(.5,1), M=(3,4);
// et des images de M par deux projections sur (AB).
pair imM1=projection(A,B,C,D)*M,
         imM2=projection(A,B)*M;

// Constructions
draw(line(A,B),blue);
draw(line(C,D),green);
draw(segment(M,imM1),dashed+green);
draw(segment(M,imM2),dashed+red); 
perpendicularmark(line(M,imM2),line(A,B),quarter=2);
dot("$A$",A,S); dot("$B$",B,NE);
dot("$C$",C,N); dot("$D$",D,SW);
dot("$M$",M,NE);
dot("$M_1$",imM1,SW,red);
dot("$M_2$",imM2,SW,red);

addMargins(1cm,1cm);

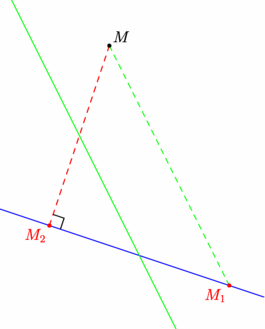
/* Projections sur une droite (objet de type line)
a) orthogonalement
    transform projection(line l)
b) parallèlement à une autre droite (objet de type line)
    transform projection(line l1, line l2, bool safe=false)
*/
// import geometry_dev; // extension devenue l'extension geometry officielle
import geometry;        // le 12/05/09, dans la version 1.71 d'asymptote. :-))

size(7cm,0);

// Définition de deux droites par leurs équations
// droite d1 d'équation x + 2y - 3 = 0
line d1=line(1,3,-3);
// droite d2 d'équation y = -2x + 3
line d2=line(-2,3);

point M=(1,2);
// Images de M par deux projections sur d1.
pair imM1=projection(d1,d2)*M,
         imM2=projection(d1)*M;

// Constructions
draw(d1,blue);
draw(d2,green);
draw(segment(M,imM1),dashed+green);
draw(segment(M,imM2),dashed+red); 
perpendicularmark(line(M,imM2),d1,quarter=2);
dot("$M$",M,NE);
dot("$M_1$",imM1,SW,red);
dot("$M_2$",imM2,SW,red);

addMargins(1cm,1cm);

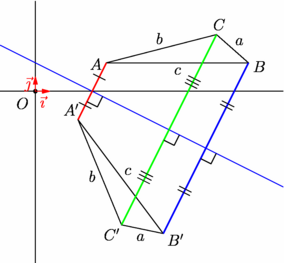
import geometry;

size(7.5cm);

show(currentcoordsys);

line axe=line(-.5,2);
triangle t=triangleabc(3,8,10,(5,2)),
         imt=reflect(axe)*t; 
// tri=triangleabc(a=3,b=8,c=10,angle=0,A=(5,2));
// tri est un triangle ABC direct, tel que :
//                     A=(5,2), 
//                     (vec(i),vec(AB))=0,
//                     a=BC=3,b=AC=8,c=AB=10
                 
draw(axe,blue);

show(t);
show("$A'$","$B'$","$C'$",imt);
draw(segment(t.A,imt.A),1bp+red,StickIntervalMarker(2,1));
draw(segment(t.B,imt.B),1bp+blue,StickIntervalMarker(2,2));
draw(segment(t.C,imt.C),1bp+green,StickIntervalMarker(2,3));
perpendicularmark(line(t.A,imt.A),axe);
perpendicularmark(line(t.B,imt.B),axe);
perpendicularmark(line(t.C,imt.C),axe);

addMargins(5mm,5mm);

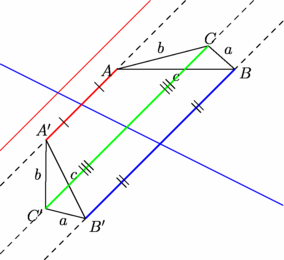
import geometry;

size(7.5cm);
line l1=line(1,0),l2=line(-.5,0);
triangle t=triangleabc(3,8,10,(5,2)),
         imt=scale(-1,l2,l1)*t; 
// tri=triangleabc(a=3,b=8,c=10,angle=0,A=(5,2));
// tri est un triangle ABC direct, tel que :
//                     A=(5,2), 
//                     (vec(i),vec(AB))=0,
//                     a=BC=3,b=AC=8,c=AB=10
                 
draw(l1,red);
draw(l2,blue);

show(t);
show("$A'$","$B'$","$C'$",imt);

draw(line(t.A,imt.A)^^line(t.B,imt.B)^^line(t.C,imt.C),dashed);

draw(segment(t.A,imt.A),1bp+red,StickIntervalMarker(2,1));
draw(segment(t.B,imt.B),1bp+blue,StickIntervalMarker(2,2));
draw(segment(t.C,imt.C),1bp+green,StickIntervalMarker(2,3));

addMargins(10mm,10mm);

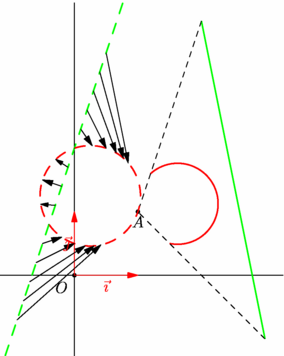
/* inversion de pôle Omega=(1,1), de puissance k=2
   M' image de M, tel que vec{AM'}.vec{AM'}=k
*/
import geometry;
size(7.5cm,0);

show(currentcoordsys);
point pA=(1,1);  // pôle d'inversion
real k=2;        // puissance de l'inversion
inversion inv=inversion(pA,k);

// Deux points pour définir un segment
point pE=(3,-1), pF=(2,4); 
segment seg=segment(pE,pF);
// et une droite d'équation y=3x+2.
line dr=line(3,2);
         
// Placement du pôle
dot("$A$",pA,S);
// Construction du segment et de son image
draw(seg,1bp+green);
draw(inv*seg,1bp+red);
draw(pE--pA--pF,dashed);
// Construction de la droite et de son image
draw(dr,1bp+dashed+green);
draw(inv*dr,1bp+dashed+red);
// Un faisceau de flèches pour montrer la transformation
// de quelques points de la droite.
for(int i=0; i<15; ++i){
        point pM=point(dr,relabscissa(-.9+i*.1));
        draw(pM--inv*pM,Arrow);
}
addMargins(5mm,5mm);