Page Asymptote du site référent / Page d'accueil de la galerie / FORUM ASYMPTOTE
POINTS, MILIEUX, BARYCENTRES (20)
Liste des figures
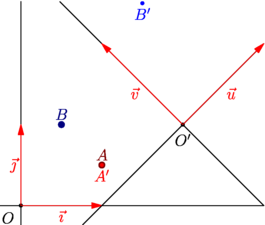
Figure fig_aa00_211109_difference_pair_point
figure 0001
Figure fig_aa01_150208_points
figure 0002
Figure fig_aa02_150208_points
figure 0003
Figure fig_aa03_150208_points
figure 0004
Figure fig_ab01_120608_suite_de_points
figure 0005
Figure fig_ab02_120608_suite_de_points
figure 0006
Figure fig_ac01_180208_tailles_de_points
figure 0007
Figure fig_ba01_180208_milieu
figure 0008
Figure fig_ba01_190611_points
figure 0009
Figure fig_ba02_180208_milieu
figure 0010
Figure fig_ba03_180208_milieu
figure 0011
Figure fig_ba04_180208_milieu
figure 0012
Figure fig_ga01_181208_barycentre
figure 0013
Figure fig_pa01_301009_points_associes
figure 0014
Figure fig_pa02_301009_points_associes
figure 0015
Figure fig_po01_271209_point_truepoint
figure 0016
Figure fig_po02_271209_point_truepoint
figure 0017
Figure fig_po03_271209_point_truepoint
figure 0018
Figure fig_po04_271209_point_truepoint
figure 0019
Figure fig_ra01_280210_points_aleatoires
figure 0020
Asymptote - Figure 0001: fig_aa00_211109_difference_pair_point.asy
(Code compilé avec Asymptote version 2.14svn)
largeur320 Figure fig_aa00_211109_difference_pair_point 
// Un exemple pour expliquer qu'il y a deux
// types possibles pour définir des points :

// - le type pair (défini nativement dans asymptote) est 
//   un couple de réels dans le repère par défaut ;
// - le type point (défini dans l'extension geometry)
//   est un couple de réels relatif à un repère choisi.

import geometry;
size(7cm,0);
// Le repère courant est currentcoordsys 
// et sa valeur par défaut est defaultcoordsys.
show(defaultcoordsys);

pair  pA=(1,.5);
point pB=(.5,1); 

dot("$A$",pA,N,5bp+.5red);
dot("$B$",pB,N,5bp+.5blue);

// On change de répertoire courant et on l'affiche.
currentcoordsys=cartesiansystem((2,1),i=(1,1),j=(-1,1));
show("$O'$","$\vec{u}$","$\vec{v}$",currentcoordsys);

// On redéfinit un "pair" et un "point" avec les mêmes coordonnées.
pair  pAp=(1,.5);
point pBp=(.5,1); 

dot("$A'$",pAp,S,3bp+red);
dot("$B'$",pBp,S,3bp+blue);
Asymptote - Figure 0002: fig_aa01_150208_points.asy
(Code compilé avec Asymptote version 1.95svn)
largeur320 Figure fig_aa01_150208_points 
// On définit la largeur de l'image ;
// la hauteur va s'adapter automatiquement pour garder les proportions.
size(6cm,0);

// Points définis par coordonnées cartésiennes
dot((0,0));
dot((2,2),pink);

// Des points particuliers
// N(0,1) au Nord, E(1,0) à l'est
// S(0,-1) au Sud, W(-1,0) à l'ouest
dot(N,blue);
dot(E,green);
dot(S,red);
dot(W,orange);
Asymptote - Figure 0003: fig_aa02_150208_points.asy
(Code compilé avec Asymptote version 1.95svn)
largeur320 Figure fig_aa02_150208_points 
// On définit la largeur de l'image ;
// la hauteur va s'adapter automatiquement
// pour garder les proportions.
size(6cm,0);

// Points définis par leurs coordonnées cartésiennes
dot((0,0));
dot((2,2),pink);

// Des points particuliers
// NE de coordonnées polaires (1,45°) au Nord-Est,
// SE de coordonnées polaires (1,-45°) au Sud-Est,
// NW de coordonnées polaires (1,135°) au Nord-Ouest,
// SW de coordonnées polaires (1,-135°) au Sud-Ouest
dot(NE,blue);
dot(SE,green);
dot(SW,red);
dot(NW,orange);

// Le point (1.5,0) peut s'écrire 1.5E
dot(1.5E,gray);
Asymptote - Figure 0004: fig_aa03_150208_points.asy
(Code compilé avec Asymptote version 1.95svn)
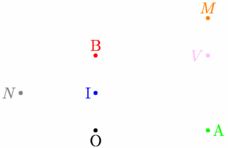
largeur320 Figure fig_aa03_150208_points 
size(6cm,0);

// Des points (ou vecteurs selon contexte)
// définis par leurs coordonnées
pair pO=(0,0), pA=(3,0), pB=(0,2);

dot("O",pO,S);
dot("A",pA,E,green);
dot("B",pB,N,red);

// I=(0,1) est une constante prédéfinie
dot("I",I,W,blue);
// ... bien utile pour définir des points
// (ou vecteur) par leur affixe :
pair pM=3+3I, pN=-2+I;
dot("$M$",pM,N,orange);
dot("$N$",pN,W,gray);

// On place le point V
// tel que vec(OV)=vec(OA)+vec(OB)
pair pV=pA+pB;
dot("$V$",pV,W,pink);
Asymptote - Figure 0005: fig_ab01_120608_suite_de_points.asy
(Code compilé avec Asymptote version 1.95svn)
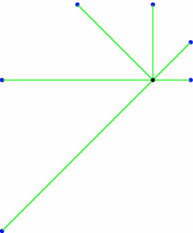
largeur320 Figure fig_ab01_120608_suite_de_points 
// On définit les unités de longueurs.
unitsize(1cm,1cm);

// Définition d'une suite de points
pair [] pA;
pA[0]=( 0, 0);
pA[1]=( 1, 0);
pA[2]=( 1, 1);
pA[3]=( 0, 2);
pA[4]=(-2, 2);
pA[5]=(-4, 0);
pA[6]=(-4,-4);

for (int i=1; i<=6; ++i) { // début d'une boucle
 dot(pA[i],blue);          //   on affiche un point
 draw(pA[0]--pA[i],green); //   on trace un segment
}                          // fin de la boucle
dot(pA[0]);
Asymptote - Figure 0006: fig_ab02_120608_suite_de_points.asy
(Code compilé avec Asymptote version 1.95svn)
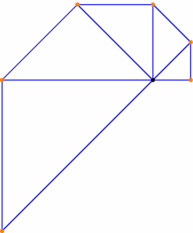
largeur320 Figure fig_ab02_120608_suite_de_points 
// On définit les unités de longueurs.
unitsize(1cm,1cm);

// Définition d'une suite de points
pair [] pA = {( 0, 0),
              ( 1, 0),
              ( 1, 1),
              ( 0, 2),
              (-2, 2),
              (-4, 0),
              (-4,-4)};

for (int i=1; i<=6; ++i) {   // début d'une boucle
 draw(pA[0]--pA[i]--pA[i-1],blue);  // une ligne brisée
 dot(pA[i-1]--pA[i],orange);        // deux points, extrémités d'un segment
 }                           // fin de la boucle
dot(pA[0]);
Asymptote - Figure 0007: fig_ac01_180208_tailles_de_points.asy
(Code compilé avec Asymptote version 1.95svn)
largeur320 Figure fig_ac01_180208_tailles_de_points 
unitsize(1cm); 

dot((0,0),red); 

real w=linewidth(); 
dot((1,0),linewidth(6w)+red);  // taille de point par défaut

dot((2,0),linewidth(10w)); 
dot((3,0),linewidth(15w));
dot((4,0),linewidth(20w)); 

// Ajout d'un cadre, distant des bords de l'image de 3mm
shipout(bbox(5mm,white));

/* remarque : on peut changer la taille de tous les points
   d'une figure en écrivant :
   dotfactor=n;
*/
Asymptote - Figure 0008: fig_ba01_180208_milieu.asy
(Code compilé avec Asymptote version 1.95svn)
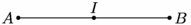
largeur320 Figure fig_ba01_180208_milieu 
// Définition de la taille de l'image
size(5cm,0);

// Définition et tracé du segment [AB]
pair A=(0,0), B=(4,0);
draw(A--B);
dot("$A$",A,W);
dot("$B$",B,E);

// Construction du milieu I de [AB]
dot("$I$",(A+B)/2,N);
Asymptote - Figure 0009: fig_ba01_190611_points.asy
(Code compilé avec Asymptote version 2.14svn)
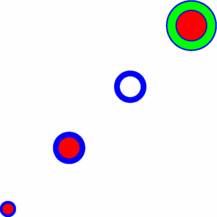
largeur320 Figure fig_ba01_190611_points 
size(5cm);

int k=0;

dot((k,k),2bp+blue,Fill(red));
dot((++k,k),4bp+blue,Fill(red));
dot((++k,k),4bp+blue,UnFill());

dot((++k,k),6bp+green,FillDraw(red,8bp+blue));
Asymptote - Figure 0010: fig_ba02_180208_milieu.asy
(Code compilé avec Asymptote version 1.95svn)
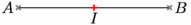
largeur320 Figure fig_ba02_180208_milieu 
// Définition de la taille de l'image
size(5cm,0);

// Définition et tracé du segment [AB]
pair A=(0,0), B=(4,0);
draw(A--B);

// Définition de styles de points
marker croix1=marker(scale(2)*cross(4),
                     1bp+gray);
marker croix2=marker(scale(2)*rotate(45)*cross(4),
                     1bp+red);

// Placement des points dans un style particulier
draw("$A$",A,W,croix1);
draw("$B$",B,E,croix1);

// Construction du milieu
draw("$I$",midpoint(A--B),S,croix2);
Asymptote - Figure 0011: fig_ba03_180208_milieu.asy
(Code compilé avec Asymptote version 1.95svn)
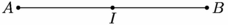
largeur320 Figure fig_ba03_180208_milieu 
/* L'extension geometry de Philippe Ivaldi définit :
 * plusieurs nouvelles structures (types) dont point et segment ;
 * une nouvelle syntaxe d'utilisation de la fonction midpoint
   spécifique aux objets de type segment.*/

// import geometry_dev; // extension devenue l'extension geometry officielle
import geometry;        // le 12/05/09, dans la version 1.71 d'asymptote. :-))

// Définition de la largeur de l'image
size(6cm,0);

// Définition et tracé du segment [AB]
point A=(0,0), B=(4,0);
segment sAB=segment(A,B);
draw(sAB);
dot("$A$",A,W);
dot("$B$",B,E);

// Construction du milieu I de [AB]
dot("$I$",midpoint(sAB),S);
Asymptote - Figure 0012: fig_ba04_180208_milieu.asy
(Code compilé avec Asymptote version 1.95svn)
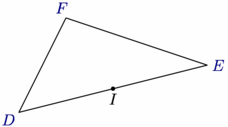
largeur320 Figure fig_ba04_180208_milieu 
/* L'extension geometry de Philippe Ivaldi définit :
 * plusieurs nouvelles structures (types) dont point, triangle et side ;
 * une nouvelle syntaxe d'utilisation de la fonction midpoint
   spécifique aux objets de type **side**.*/

// import geometry_dev; // extension devenue l'extension geometry officielle
import geometry;        // le 12/05/09, dans la version 1.71 d'asymptote. :-))
     
// Définition de la largeur de l'image
size(6cm,0);

// Définition du triangle EFG
point pE=(0,0),pF=(4,1),pG=(1,2);
triangle t=triangle(pE,pF,pG);
draw(t);label("$D$","$E$","$F$",t,.5blue);

// On définit c1 comme "premier" côté de t
side c1=t.AB;

// On construit I milieu de [EF]
dot("$I$",midpoint(c1),S);
Asymptote - Figure 0013: fig_ga01_181208_barycentre.asy
(Code compilé avec Asymptote version 1.95svn)
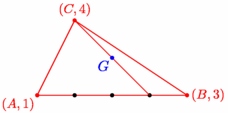
largeur320 Figure fig_ga01_181208_barycentre 
// Définition de la taille de l'image
size(6cm,0);

defaultpen(fontsize(10pt)+red); // Stylo par défaut

// Définitions
pair pA=(0,0), pB=(4,0),  pC=(1,2);
real a=1, b=3, c=4;
path tri=pA--pB--pC--cycle;
pair pG=(a*pA+b*pB+c*pC)/(a+b+c),
     pH=(a*pA+b*pB)/(a+b);

// Tracés
draw(tri);
dot("$(A,1)$",pA,SW);
dot("$(B,3)$",pB,E);
dot("$(C,4)$",pC,N);
for (int k=1; k<=3; ++k) {
    dot(relpoint(pA--pB,k/4),black);
}
draw(pH--pC);
dot("$G$",pG,SW,fontsize(11pt)+blue);
Asymptote - Figure 0014: fig_pa01_301009_points_associes.asy
(Code compilé avec Asymptote version 1.95svn)
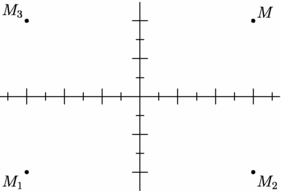
largeur320 Figure fig_pa01_301009_points_associes 
// Fonction "conjugué" : pair conj(pair z)

import graph;
unitsize(1cm);

pair pO=(0,0), pM=(3,2);

pair pM1=-pM,       // symétrique par rapport à l'origine
     pM2=conj(pM),  // symétrique par rapport à l'axe (Ox)
     pM3=conj(-pM); // symétrique par rapport à l'axe (Oy)

// D'autres possibilités pour le conjugué :
// pM2=(pM.x,-pM.y)
// pM2=pM.x-I*pM.y        I=(0,1)
         
xaxis(Ticks(format="%"));
yaxis(Ticks(format="%"));
         
dot("$M$",pM,NE);
dot("$M_1$",pM1,SW);
dot("$M_2$",pM2,SE);
dot("$M_3$",pM3,NW);
Asymptote - Figure 0015: fig_pa02_301009_points_associes.asy
(Code compilé avec Asymptote version 1.95svn)
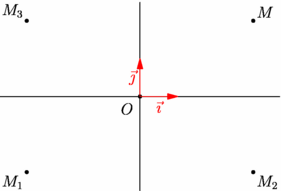
largeur320 Figure fig_pa02_301009_points_associes 
// Le même exemple que le précédent
// en utilisant des fonctions de l'extension geometry.
import geometry;
import graph;
unitsize(1cm);

point pO=(0,0), pM=(3,2);

transform sO=scale(-1,pO), // symétrie par rapport à O (homothétie de rapport -1)
          sOx=reflect(Ox), // réflexion d'axe (Ox)
          sOy=reflect(Oy); // réflexion d'axe (Oy)

// autre possibilité : sO=rotateO(180)
                  
point pM1=sO*pM,  // image de pM par sO
      pM2=sOx*pM, // image de pM par sOx
      pM3=sOy*pM; // image de pM par sOy

show(defaultcoordsys);
         
dot("$M$",pM,NE);
dot("$M_1$",pM1,SW);
dot("$M_2$",pM2,SE);
dot("$M_3$",pM3,NW);
Asymptote - Figure 0016: fig_po01_271209_point_truepoint.asy
(Code compilé avec Asymptote version 1.95svn)
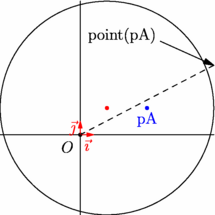
largeur320 Figure fig_po01_271209_point_truepoint 
/* Attention, aux fonctions point et truepoint !
   Elles ne font pas forcément ce que l'on pourrait croire.
*/

import geometry;

unitsize(10); // 10 bp = 10/72 pouce = 254/72 mm

show(defaultcoordsys);

pair pA=(5,2), pC=(2,2);

draw(circle(pC,8));
dot(pC,red);

dot("pA",pA,S,blue);
draw((0,0)--point(pA),dashed);

draw(Label("point(pA)",W),(6,7)--point(pA),Arrow);
Asymptote - Figure 0017: fig_po02_271209_point_truepoint.asy
(Code compilé avec Asymptote version 1.95svn)
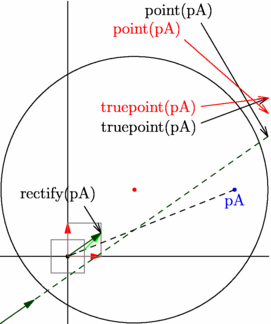
largeur320 Figure fig_po02_271209_point_truepoint 
/* Attention, aux fonctions point et truepoint !
   Elles ne font pas forcément ce que l'on pourrait croire.
*/

import geometry;

unitsize(25); // 25 bp = 25/72 pouce = (25*25,4)/72 mm

show("","","",defaultcoordsys);

pair pA=(5,2), pC=(2,2);

draw(shift(-.5,-.5)*unitsquare,gray);
draw(unitsquare,gray);

draw(circle(pC,4));
dot(pC,red);

dot("pA",pA,S,blue);
draw(pA--(0,0)--rectify(pA)-(0.5,0.5),dashed);
draw(rectify(pA)-(0.5,0.5)--rectify(pA),green,Arrow);
draw((0,0)--rectify(pA),darkgreen,Arrow);
draw(truepoint(SW)--truepoint(SW)+rectify(pA),darkgreen,Arrow);
draw(truepoint(SW)--point(pA),dashed+darkgreen);

draw(Label("rectify(pA)",W),(.5,1.5)--rectify(pA),Arrow(SimpleHead));
draw(Label("point(pA)",W),(4,7)--point(pA),Arrow(SimpleHead));
draw(Label("truepoint(pA)",W),(4,4)--truepoint(pA),Arrow(SimpleHead));
draw(Label("point(pA)",W),(3.5,6.5)--point(pA),red,Arrow(SimpleHead));
draw(Label("truepoint(pA)",W),(4,4.5)--truepoint(pA),red,Arrow(SimpleHead));
Asymptote - Figure 0018: fig_po03_271209_point_truepoint.asy
(Code compilé avec Asymptote version 1.95svn)
largeur320 Figure fig_po03_271209_point_truepoint 
/* Attention, aux fonctions point et truepoint !
   Elles ne font pas forcément ce que l'on pourrait croire.
*/

import geometry;

unitsize(25); // 25 bp = 25/72 pouce = (25*25,4)/72 mm

show("","","",defaultcoordsys);

pair pA=(2,5), pC=(2,2);

draw(shift(-.5,-.5)*unitsquare,gray);
draw(unitsquare,gray);

draw(circle(pC,4));
dot(pC,red);

dot("pA",pA,NW,blue);
draw(pA--(0,0)--rectify(pA)-(0.5,0.5),dashed);
draw(rectify(pA)-(0.5,0.5)--rectify(pA),green,Arrow);
draw((0,0)--rectify(pA),darkgreen,Arrow);
draw(truepoint(SW)--truepoint(SW)+rectify(pA),darkgreen,Arrow);
draw(truepoint(SW)--point(pA),dashed+darkgreen);

draw(Label("rectify(pA)",W),(2.5,1.5)--rectify(pA),Arrow(SimpleHead));
draw(Label("point(pA)",W),(5,4.5)--point(pA),Arrow(SimpleHead));
draw(Label("truepoint(pA)",W),(4,3.5)--truepoint(pA),Arrow(SimpleHead));
draw(Label("point(pA)",W),(5.5,5)--point(pA),red,Arrow(SimpleHead));
draw(Label("truepoint(pA)",W),(4.5,3)--truepoint(pA),red,Arrow(SimpleHead));
Asymptote - Figure 0019: fig_po04_271209_point_truepoint.asy
(Code compilé avec Asymptote version 1.95svn)
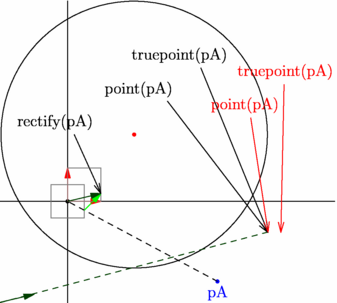
largeur320 Figure fig_po04_271209_point_truepoint 
/* Attention, aux fonctions point et truepoint !
   Elles ne font pas forcément ce que l'on pourrait croire.
*/

import geometry;

unitsize(25); // 25 bp = 25/72 pouce = (25*25,4)/72 mm

show("","","",defaultcoordsys);

pair pA=(4.5,-2.4), pC=(2,2);

draw(shift(-.5,-.5)*unitsquare,gray);
draw(unitsquare,gray);

draw(circle(pC,4));
dot(pC,red);

dot("pA",pA,S,blue);
draw(pA--(0,0)--rectify(pA)-(0.5,0.5),dashed);
draw(rectify(pA)-(0.5,0.5)--rectify(pA),green,Arrow);
draw((0,0)--rectify(pA),darkgreen,Arrow);
draw(truepoint(SW)--truepoint(SW)+rectify(pA),darkgreen,Arrow);
draw(truepoint(SW)--truepoint(pA),dashed+darkgreen);

draw(Label("rectify(pA)",W),(.2,2)--rectify(pA),Arrow(SimpleHead));
draw(Label("point(pA)",W),(3,3)--point(pA),Arrow(SimpleHead));
draw(Label("truepoint(pA)",W),(4,4)--truepoint(pA),Arrow(SimpleHead));
draw(Label("point(pA)",W),(5.5,2.5)--point(pA),red,Arrow(SimpleHead));
draw(Label("truepoint(pA)",W),(6.5,3.5)--truepoint(pA),red,Arrow(SimpleHead));
Asymptote - Figure 0020: fig_ra01_280210_points_aleatoires.asy
(Code compilé avec Asymptote version 1.95svn)
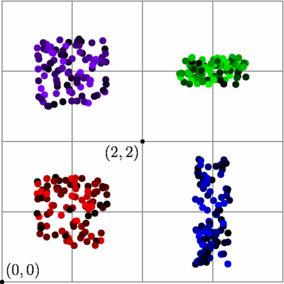
largeur320 Figure fig_ra01_280210_points_aleatoires 
import math;

size(7.5cm);

add(grid(4,4,gray));

pair aleapair(real x, real y, real Dx, real Dy=Dx){
         return (x+(2*unitrand()-1)*Dx,y+(2*unitrand()-1)*Dy);
}
pair aleapair(pair pt, real Dx, real Dy=Dx){
         return (pt.x+(2*unitrand()-1)*Dx,pt.y+(2*unitrand()-1)*Dy);
}

srand((int)time("%S"));
for(int k=0; k<100; ++k){
    dot(aleapair(x=1,y=1,Dx=.5),5bp+unitrand()*red);
    dot(aleapair(3,1,.25,.75),5bp+unitrand()*blue);
    dot(aleapair(3,3,.5,.2),5bp+unitrand()*green);
    dot(aleapair(pt=(1,3),.5),5bp+unitrand()*purple);
}
dot("$(0,0)$",(0,0),NE);
dot("$(2,2)$",(2,2),SW);
Page Asymptote du site référent / Page d'accueil de la galerie / FORUM ASYMPTOTE

Dernière modification le Fri Oct 28 12:59:03 CEST 2011 par G.Marris       Valide XHTML