Page Asymptote du site référent / Page d'accueil de la galerie / FORUM ASYMPTOTE
LIGNES, DROITES, SEGMENTS (41)
Liste des figures
Figure fig_aa01_150208_segments
figure 0001
Figure fig_aa02_150208_segments
figure 0002
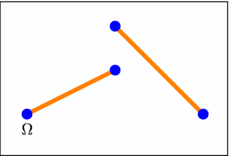
Figure fig_aa03_190208_segments
figure 0003
Figure fig_ab01_150208_stylos
figure 0004
Figure fig_ab02_010808_stylos
figure 0005
Figure fig_ac01_040409_stylos
figure 0006
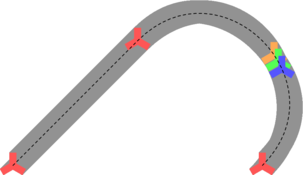
Figure fig_ad01_150112_stylo_makepen
figure 0007
Figure fig_da01_220208_droite
figure 0008
Figure fig_da02_220208_droite
figure 0009
Figure fig_da03_080308_droite
figure 0010
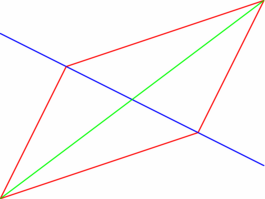
Figure fig_db01_080308_droites
figure 0011
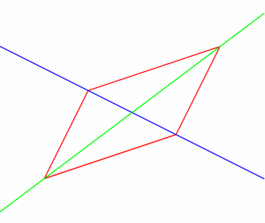
Figure fig_db02_080308_droites
figure 0012
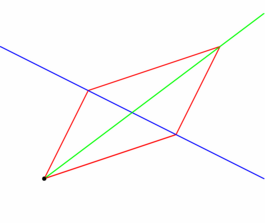
Figure fig_db03_080308_droites
figure 0013
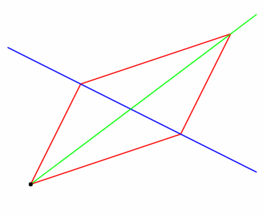
Figure fig_db04_090308_droites
figure 0014
Figure fig_ea01_220208_droite_equation
figure 0015
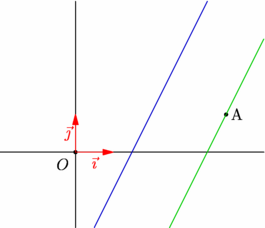
Figure fig_fa01_090308_droite_parallele
figure 0016
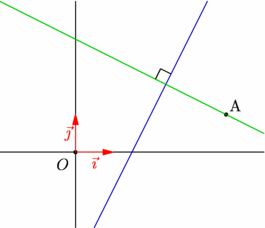
Figure fig_ga01_090308_droite_perpendiculaire
figure 0017
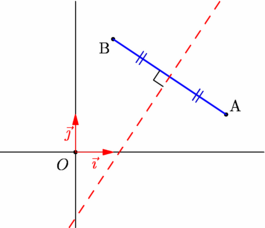
Figure fig_ga02_090308_mediatrice
figure 0018
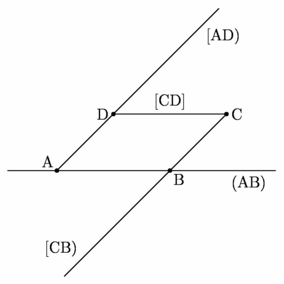
Figure fig_lb01_180208_line_A_B
figure 0019
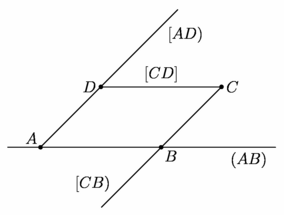
Figure fig_lb02_090308_line_A_B
figure 0020
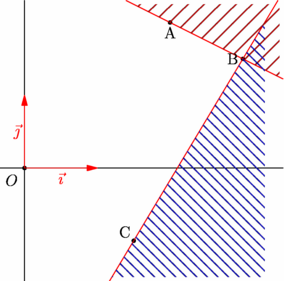
Figure fig_lb03_281209_line_A_B_hachures
figure 0021
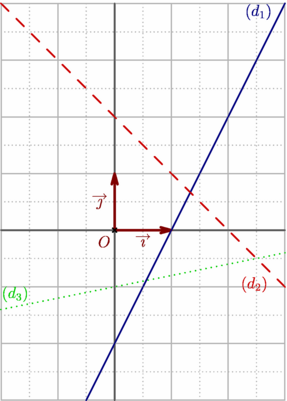
Figure fig_mb01_180208_line_m_p
figure 0022
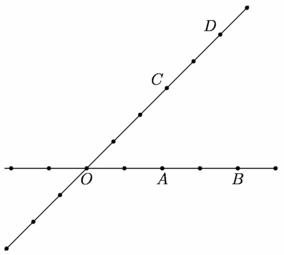
Figure fig_na01_060708_droite_graduee
figure 0023
Figure fig_na02_060708_droite_graduee
figure 0024
Figure fig_pa01_010808_path
figure 0025
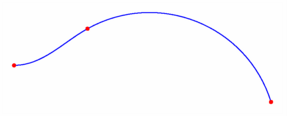
Figure fig_pa02_010808_path
figure 0026
Figure fig_pa03_010808_path
figure 0027
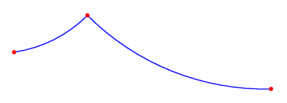
Figure fig_pa04_010808_path
figure 0028
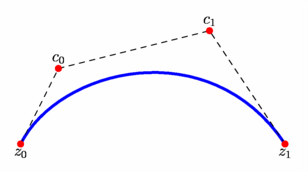
Figure fig_pb01_291009_path_Bezier
figure 0029
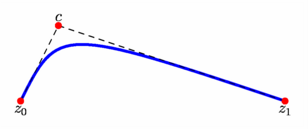
Figure fig_pb02_291009_path_Bezier
figure 0030
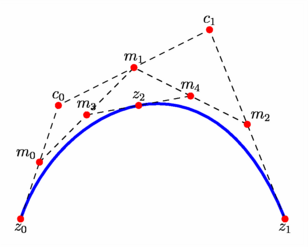
Figure fig_pb03_291009_path_Bezier
figure 0031
Figure fig_pb04_291009_path_Bezier
figure 0032
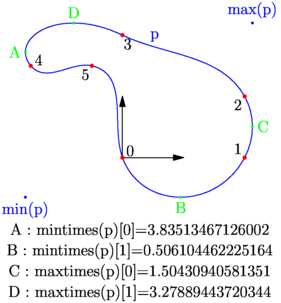
Figure fig_pm01_271011_path_min_max
figure 0033
Figure fig_pt01_271011_path_times
figure 0034
Figure fig_pt02_271011_path_times
figure 0035
Figure fig_sa01_051111_bspline_accel
figure 0036
Figure fig_si01_160812_size_length
figure 0037
Figure fig_ta00_211112_time
figure 0038
Figure fig_ta01_010808_arctime
figure 0039
Figure fig_tb01_010808_dirtime
figure 0040
Figure fig_tc01_010808_reltime
figure 0041
Asymptote - Figure 0001: fig_aa01_150208_segments.asy
(Code compilé avec Asymptote version 2.14svn)
largeur320 Figure fig_aa01_150208_segments 
// définition de l'unité de longueur 
unitsize(1cm);

// on trace un segment défini par les coordonnées de ses extrémités
draw ((0,0)--(6,1));

// un deuxième segment d'un trait plus épais
draw ((0,0)--(5,2),linewidth(4bp));

// un troisième vert et d'une épaisseur intermédiaire
draw ((0,0)--(4,4),green+2bp);
Asymptote - Figure 0002: fig_aa02_150208_segments.asy
(Code compilé avec Asymptote version 1.95svn)
largeur320 Figure fig_aa02_150208_segments 
// On définit la largeur de l'image ;
// la hauteur va s'adapter pour garder les proportions.
size(7cm,0);

// définition de 4 "points" (couples de coordonnées)
// NB : ces couples pourraient aussi caractériser des vecteurs
pair A, B, C, D;
A=(0,0);
B=(2,1);
C=(2,2);
D=(4,0);

// on trace [AB] de couleur rouge
draw(A--B,red);

// et [CD] d'un trait plus épais et bleu
draw(C--D,blue+3bp);
Asymptote - Figure 0003: fig_aa03_190208_segments.asy
(Code compilé avec Asymptote version 1.95svn)
largeur320 Figure fig_aa03_190208_segments 
// On définit la largeur de l'image ;
// la hauteur va s'adapter pour garder les proportions.
size(6cm,0);

// définition de 4 "points" (couples de coordonnées)
// NB : ces couples pourraient aussi caractériser des vecteurs
pair pA=(0,0),pB=(2,1),pC=(2,2),pD=(4,0);
// on trace deux segments avec le même stylo orange
draw(pA--pB^^pC--pD,orange+3bp);
// on place de gros points bleus :-)
dot(pA--pB^^pC--pD,blue+8bp);
// et on étiquette l'un des points
label("$\Omega$",pA,2S);

// Ajout d'un cadre, distant des bords de l'image de 5mm
shipout(bbox(5mm));
Asymptote - Figure 0004: fig_ab01_150208_stylos.asy
(Code compilé avec Asymptote version 1.95svn)
largeur320 Figure fig_ab01_150208_stylos 
// définition de l'unité de longueur
unitsize(1cm);

draw ((0,5)--(7,5),solid+blue+1bp);
draw ((0,4)--(7,4),dotted+.5blue+1bp);
draw ((0,3)--(7,3),dashed+red+1bp);
draw ((0,2)--(7,2),longdashed+.5red+1bp);
draw ((0,1)--(7,1),dashdotted+green+1bp);
draw ((0,0)--(7,0),longdashdotted+.5green+1bp);

// Ajout d'un cadre, distant des bords de l'image de 3mm
shipout(bbox(3mm));
Asymptote - Figure 0005: fig_ab02_010808_stylos.asy
(Code compilé avec Asymptote version 2.14svn)
largeur320 Figure fig_ab02_010808_stylos 
/* Styles prédéfinis
pen solid=linetype("");
pen dotted=linetype("0 4");
pen dashed=linetype("8 8");
pen longdashed=linetype("24 8");
pen dashdotted=linetype("8 8 0 8");
pen longdashdotted=linetype("24 8 0 8");
pen Dotted=dotted+1.0;
pen Dotted(pen p=currentpen) {return dotted+2*linewidth(p);}
*/

unitsize(1cm);

// définir ses propres styles de traits

draw ((0,5)--(7,5),linetype(""));
draw ((0,4)--(7,4),linetype("0 4"));
draw ((0,3)--(7,3),linetype("8 8"));
draw ((0,2)--(7,2),linetype("24 8"));
draw ((0,1)--(7,1),linetype("8 8 0 8"));
draw ((0,0)--(7,0),Dotted);

pen dd=linetype("0 4 4 4");
draw ((0,-1)--(7,-1),dd);

// Ajout d'un cadre, distant des bords de l'image de 3mm
shipout(bbox(3mm));
Asymptote - Figure 0006: fig_ac01_040409_stylos.asy
(Code compilé avec Asymptote version 1.95svn)
largeur320 Figure fig_ac01_040409_stylos 
unitsize(1cm);

transform t=shift(0,-1);

path p=(0,0)--(1,1)--(2,0)--(3,1)--(4,0);

draw(p,10bp+squarecap); // pen squarecap=linecap(0);
draw(t*p,10bp+roundcap); // pen roundcap=linecap(1);
draw(t^2*p,10bp+extendcap); // pen extendcap=linecap(2);

draw(t^4*p,10bp+miterjoin); // pen miterjoin=linejoin(0);
draw(t^5*p,10bp+roundjoin); // pen roundjoin=linejoin(1);
draw(t^6*p,10bp+beveljoin); // pen beveljoin=linejoin(2);

shipout(bbox(5mm));
Asymptote - Figure 0007: fig_ad01_150112_stylo_makepen.asy
(Code compilé avec Asymptote version 2.14svn)
largeur320 Figure fig_ad01_150112_stylo_makepen 
size(8cm,0);

path profil=cross(3,round=false,r=0.3),
     p=(0,0)---(1,1)..(2,0);
pen stylo=makepen(scale(10)*profil)+grey;

draw(p,stylo);
dot(p,stylo+red);

dot(point(p,1.57),stylo+orange);
dot(point(p,1.6),stylo+green);
dot(point(p,1.63),stylo+blue);

draw(p,linetype("4 4"));
Asymptote - Figure 0008: fig_da01_220208_droite.asy
(Code compilé avec Asymptote version 1.95svn)
largeur320 Figure fig_da01_220208_droite 
// On définit la largeur de l'image ;
// la hauteur va s'adapter pour garder les proportions.
size(7cm,0);

// définition de 2 couples de coordonnées
pair pA=(1,1),pB=(4,0);
// Construction des points correspondants
dot("$A$",pA,N);
dot("$B$",pB,N);

// On trace la droite (AB)
draw(interp(pA,pB,-.5)--interp(pA,pB,1.25));
// interp(pA,pB,-.5) désigne le point M de (AB)\[AB)
// vec{AM}=-0,5 vec{AB}
// interp(pA,pB,1.25) désigne le point N de (AB)\[BA)
// vec{AN}=1,25 vec{AB}
Asymptote - Figure 0009: fig_da02_220208_droite.asy
(Code compilé avec Asymptote version 1.95svn)
largeur320 Figure fig_da02_220208_droite 
// la même figure que précédemment en exploitant
// l'extension geometry de Philippe Ivaldi

// import geometry_dev; // extension devenue l'extension geometry officielle
import geometry;        // le 12/05/09, dans la version 1.71 d'asymptote. :-))

size(7cm,0);
// Notez le paramètre suivant, par défaut est à 0, qui permet de définir la
// distance des représentations de droites par rapport aux bords de l'image.
linemargin =-1cm;
// Avec une valeur négative, cela aggrandit la taille de l'image.
// Plus pratique : addmargins, à voir dans des exemples qui suivent.

// définition de 2 points
point pA=(1,1),pB=(4,0);
// Construction des points correspondants
dot("$A$",pA,SW);
dot("$B$",pB,NE);

// On trace la droite (AB)
draw(line(pA,pB));
Asymptote - Figure 0010: fig_da03_080308_droite.asy
(Code compilé avec Asymptote version 1.95svn)
largeur320 Figure fig_da03_080308_droite 
// Encore la même figure...

// import geometry_dev; // extension devenue l'extension geometry officielle
import geometry;        // le 12/05/09, dans la version 1.71 d'asymptote. :-))

size(7cm,0);
point pA=(1,1),pB=(4,0);
dot("$A$",pA,SW);
dot("$B$",pB,NE);
draw(line(pA,pB));
/* Plus pratique qu'un linemargin négatif utilisé précédemment
   ou que la solution d'un cadre invisible, on pensera à utiliser :
   addMargins(picture pic=currentpicture,
                  real lmargin=0, real bmargin=0,
                  real rmargin=lmargin, real tmargin=bmargin,
                  bool rigid=true, bool allObject=true)
*/
addMargins(1cm,1cm);
// et on peut en plus utiliser linemargin, mais positif cette fois
// pour que les droites n'aillent pas jusqu'aux bords de l'image.
linemargin=2mm;
Asymptote - Figure 0011: fig_db01_080308_droites.asy
(Code compilé avec Asymptote version 1.95svn)
largeur320 Figure fig_db01_080308_droites 
// import geometry_dev; // extension devenue l'extension geometry officielle
import geometry;        // le 12/05/09, dans la version 1.71 d'asymptote. :-))

size(7cm,0);

// définition de 4 points
point pA=(1,1),pB=(4,2),pC=(5,4),pD=(2,3);
// ... et construction du quadrilatère
draw(pA--pB--pC--pD--cycle,red);
// On trace la droite passant par pB et pD, en bleu.
draw(line(pB,pD),blue);
// ... et la droite passant par pA et pC, en vert
draw(line(pA,pC),green);
// La boundingbox (fenêtre d'affichage) est définie
// par les coordonnées extrêmes des points...
Asymptote - Figure 0012: fig_db02_080308_droites.asy
(Code compilé avec Asymptote version 1.95svn)
largeur320 Figure fig_db02_080308_droites 
// import geometry_dev; // extension devenue l'extension geometry officielle
import geometry;        // le 12/05/09, dans la version 1.71 d'asymptote. :-))

size(7cm,0);

// même figure que précédemment...
point pA=(1,1),pB=(4,2),pC=(5,4),pD=(2,3);
draw(pA--pB--pC--pD--cycle,red);
draw(line(pB,pD),blue);
draw(line(pA,pC),green);
// mais on définit un cadre invisible
draw(box((0,0),(6,5)), invisible);
Asymptote - Figure 0013: fig_db03_080308_droites.asy
(Code compilé avec Asymptote version 1.95svn)
largeur320 Figure fig_db03_080308_droites 
// import geometry_dev; // extension devenue l'extension geometry officielle
import geometry;        // le 12/05/09, dans la version 1.71 d'asymptote. :-))

size(7cm,0);
// même figure que précédemment...
point pA=(1,1),pB=(4,2),pC=(5,4),pD=(2,3);
draw(pA--pB--pC--pD--cycle,red);
draw(line(pB,pD),blue);

// cette fois, avec l'indication false suivant pA
// on obtient une demi-droite.
draw(line(pA,false,pC),green);
// un point noir pour indiquer pA
dot(pA);
// On définit un cadre invisible
draw(box((0,0),(6,5)), invisible);
Asymptote - Figure 0014: fig_db04_090308_droites.asy
(Code compilé avec Asymptote version 1.95svn)
largeur320 Figure fig_db04_090308_droites 
// import geometry_dev; // extension devenue l'extension geometry officielle
import geometry;        // le 12/05/09, dans la version 1.71 d'asymptote. :-))

size(7cm,0);
// même figure que précédemment...
point pA=(1,1),pB=(4,2),pC=(5,4),pD=(2,3);
draw(pA--pB--pC--pD--cycle,red);
draw(line(pB,pD),blue);
draw(line(pA,false,pC),green);
dot(pA);
// ... mais plus pratique qu'un linemargin négatif utilisé précédemment
// ou que la solution d'un cadre invisible, on pensera à utiliser :
// addMargins(picture pic=currentpicture,
//                      real lmargin=0, real bmargin=0,
//                      real rmargin=lmargin, real tmargin=bmargin,
//                      bool rigid=true, bool allObject=true)
addMargins(1cm,1cm);
// et on pourra en plus utiliser linemargin, mais positif cette fois
// pour que les droites n'aillent pas jusqu'aux bords de l'image.
linemargin=2mm;
Asymptote - Figure 0015: fig_ea01_220208_droite_equation.asy
(Code compilé avec Asymptote version 1.95svn)
largeur320 Figure fig_ea01_220208_droite_equation 
/* Droite définie par équation cartésienne ax+by+c=0  dans le repère R
   Syntaxe : line line(coordsys R=currentcoordsys, real a, real b, real c)
   ou
   Droite définie par équation réduite y=mx+p dans le repère R
   Syntaxe : line line(coordsys R=currentcoordsys, real slope, real origin)
*/

// import geometry_dev; // extension devenue l'extension geometry officielle
import geometry;        // le 12/05/09, dans la version 1.71 d'asymptote. :-))

size(7cm,0);

// Affichage du repère courant
show(currentcoordsys);
// Tracé de la droite d'équation x + 2y - 3 = 0
line d1=line(1,3,-3);
draw(d1,blue);
// Tracé de la droite d'équation y = 2x - 3
line d2=line(2,-3);
draw(d2,.8green);
// Point d'intersection des deux droites
dot("I",intersectionpoint(d1,d2),N,.7red);

draw(box((-2,-2),(5,4)),invisible);
Asymptote - Figure 0016: fig_fa01_090308_droite_parallele.asy
(Code compilé avec Asymptote version 1.95svn)
largeur320 Figure fig_fa01_090308_droite_parallele 
/* Droite parallèle à une droite donnée
   passant par un point donné
*/

// import geometry_dev; // extension devenue l'extension geometry officielle
import geometry;        // le 12/05/09, dans la version 1.71 d'asymptote. :-))

size(7cm,0);

// Affichage du repère courant
show(currentcoordsys);
// Tracé de la droite d'équation y = 2x - 3
line d1=line(2,-3);
draw(d1,.8blue);
// Point A de coordonnées (4,1)
point pA=(4,1);
dot("A",pA);
// Parallèle à d1 passant par A
line d2=parallel(pA,d1);
draw(d2,.8green);

draw(box((-2,-2),(5,4)),invisible);
Asymptote - Figure 0017: fig_ga01_090308_droite_perpendiculaire.asy
(Code compilé avec Asymptote version 1.95svn)
largeur320 Figure fig_ga01_090308_droite_perpendiculaire 
/* Droite perpendiculaire à une droite donnée
   passant par un point donné
*/
// import geometry_dev; // extension devenue l'extension geometry officielle
import geometry;        // le 12/05/09, dans la version 1.71 d'asymptote. :-))

size(7cm,0);

// Affichage du repère courant
show(currentcoordsys);
// Tracé de la droite d'équation y = 2x - 3
line d1=line(2,-3);
draw(d1,.8blue);
// Point A de coordonnées (4,1)
point pA=(4,1);
dot("A",pA,NE);
// Perpendiculaire à d1 passant par A
line d2=perpendicular(pA,d1);
draw(d2,.8green);
// Codage de l'angle droit
perpendicularmark(d1,d2);

draw(box((-2,-2),(5,4)),invisible);
Asymptote - Figure 0018: fig_ga02_090308_mediatrice.asy
(Code compilé avec Asymptote version 1.95svn)
largeur320 Figure fig_ga02_090308_mediatrice 
/* Médiatrice d'un segment
   en utilisant la fonction bisector de l'extension geometry_dev.
*/
// import geometry_dev; // extension devenue l'extension geometry officielle
import geometry;        // le 12/05/09, dans la version 1.71 d'asymptote. :-))

size(7cm,0);

// Affichage du repère courant
show(currentcoordsys);
// Définition de deux points A et B
point pA=(4,1), pB=(1,3);
// ... puis de la médiatrice de [AB]
line medAB=bisector(pA,pB);

// On trace le tout :
dot("A",pA,NE);
dot("B",pB,SW);
draw(pA--pB,1bp+blue,StickIntervalMarker(2,2, 0.8*blue));
draw(medAB,dashed+.8bp+red);

// Codage de l'angle droit
perpendicularmark(line(pA,pB),medAB);

draw(box((-2,-2),(5,4)),invisible);
Asymptote - Figure 0019: fig_lb01_180208_line_A_B.asy
(Code compilé avec Asymptote version 1.95svn)
largeur320 Figure fig_lb01_180208_line_A_B 
/* Un exemple commenté issu de la documentation
   de l'extension geometry de Ph. Ivaldi
   illustrant des emplois possibles
   de la fonction **line**
   (à ne pas confondre avec le type **line**).
*/
// import geometry_dev; // extension devenue l'extension geometry officielle
import geometry;        // le 12/05/09, dans la version 1.71 d'asymptote. :-))

size(7.5cm,0);
// Pour que les lignes n'aillent pas jusqu'aux bords de l'image : 
linemargin=2mm;
// Définition et placement de 4 points :
point A=(0,0), B=(2, 0), C=(3,1), D=(1,1);
dot("A", A, NW); dot("B", B, SE); 
dot("C", C); dot("D", D, W);
// Définition d'une droite
line AB=line(A, B);
// Définition d'une demi-droite
line CB=line(C, false, B);
// Définition d'un segment
line CD=line(C, false, D, false);
// Définition d'une demi-droite
line AD=line(A, false, D);
// Tracé des lignes précédentes
draw("(AB)", AB); draw("[CB)", CB);
draw(Label("[CD]",Relative(0.5),align=N), CD);
draw("[AD)", AD);
// Un cadre invisible pour définir la zone à afficher.
draw(box((-1,-2),(4,3)),invisible);
Asymptote - Figure 0020: fig_lb02_090308_line_A_B.asy
(Code compilé avec Asymptote version 1.95svn)
largeur320 Figure fig_lb02_090308_line_A_B 
/* Même figure que précédemment avec 2 différences :
   - des labels au format mathématique de LaTeX
   - utilisation de addMargins pour définir la zone d'affichage.
*/
// import geometry_dev; // extension devenue l'extension geometry officielle
import geometry;        // le 12/05/09, dans la version 1.71 d'asymptote. :-))

size(7.5cm,0);
point A=(0,0), B=(2, 0), C=(3,1), D=(1,1);
dot("$A$", A, NW); dot("$B$", B, SE); 
dot("$C$", C); dot("$D$", D, W);
line AB=line(A, B);
line CB=line(C, false, B);
line CD=line(C, false, D, false);
line AD=line(A, false, D);

draw("$(AB)$", AB);
draw("$[CB)$", CB);
draw(Label("$[CD]$",Relative(0.5),align=N), CD);
draw("$[AD)$", AD);

// Marge de 1cm à gauche du point le plus à gauche
// Marge de 2cm en dessous du point le plus bas
// Marge de 1.5cm à droite du point le plus à droite
// Marge de 2.5cm au dessus du point le plus haut
addMargins(1cm,2cm,1.5cm,2.5cm);
// et je remets linemargin pour que les droites n'aillent pas
// jusqu'aux bords de l'image
linemargin = 2mm;
Asymptote - Figure 0021: fig_lb03_281209_line_A_B_hachures.asy
(Code compilé avec Asymptote version 1.95svn)
largeur320 Figure fig_lb03_281209_line_A_B_hachures 
import geometry;
import patterns;
size(7.5cm,0);

// On définit :
point pA=(2,2), pB=(3,1.5), pC=(1.5,-1);

line droite1=line(pA,pB);
segment bord1=segment(relpoint(droite1,-.5),relpoint(droite1,1.5));
path zonehachuree1=bord1.A--bord1.B--(bord1.B.x,bord1.A.y)--cycle;

line droite2=line(pB,pC);
segment bord2=segment(relpoint(droite2,-.2),relpoint(droite2,1.2));
path zonehachuree2=bord2.A--bord2.B--(bord2.A.x,bord2.B.y)--cycle;

// On trace :
show(currentcoordsys);
dot("A",pA,S);
dot("B",pB,W);
dot("C",pC,NW);
draw(droite1^^droite2,red);
add("hachure1",hatch(H=3mm,dir=NE,red));
fill(zonehachuree1,pattern("hachure1"));
add("hachure2",hatch(H=2mm,dir=NW,blue));
fill(zonehachuree2,pattern("hachure2"));

addMargins(.1cm,.1cm);
Asymptote - Figure 0022: fig_mb01_180208_line_m_p.asy
(Code compilé avec Asymptote version 1.95svn)
largeur320 Figure fig_mb01_180208_line_m_p 
// import geometry_dev; // extension devenue l'extension geometry officielle
import geometry;        // le 12/05/09, dans la version 1.71 d'asymptote. :-))

import graph_pi;

unitsize(1.5cm,1.5cm);

scale(false);
real xmin=-2, xmax=3, ymin=-3, ymax=4;
grid(xmin, xmax, ymin, ymax,
     xStep=1, xstep=.5,
     yStep=1, ystep=.5,
     pTick=.7bp+.7white,
     ptick=.7bp+dotted+.7white,
     above=false
     );
draw((xmin,0)--(xmax,0)^^(0,ymin)--(0,ymax),
     1.3bp+0.7*grey);
labeloij(p=1.7bp+.5*red,
         arrow=Arrow(SimpleHead,8bp),
         scale(2)*Mark(5)
         );
line d1=line(2,-2);
draw(Label("$(d_1)$",Relative(.95),align=NW), d1,
     1bp+solid+.5blue);
line d2=line(-1,2);
draw(Label("$(d_2)$",Relative(.95),align=SW), d2,
     1bp+dashed+.8red);
line d3=line(1/5,-1);
draw(Label("$(d_3)$",Relative(.05),align=N), d3,
     1bp+dotted+.8green);
Asymptote - Figure 0023: fig_na01_060708_droite_graduee.asy
(Code compilé avec Asymptote version 1.95svn)
largeur320 Figure fig_na01_060708_droite_graduee 
// import geometry_dev; // extension devenue l'extension geometry officielle
import geometry;        // le 12/05/09, dans la version 1.71 d'asymptote. :-))

unitsize(1cm);

// ~~~~~~ DEFINITIONS ~~~~~~~~~~~~~~~~~~~~~~

pair pO=(0,0), pI=(1,0), pJ=rotate(45,pO)*pI;
line d1 = line(pO,pI);
line d2 = line(pO,pJ);

// Définition d'un repère non orthogonal
currentcoordsys = cartesiansystem(pO,i=pI,j=pJ);

int n1min=-2, n1max=5, n2min=-3, n2max=6;

point pA=(2,0), pB=(4,0), pC=(0,3), pD=(0,5);

// ~~~~~~ CONSTRUCTIONS ~~~~~~~~~~~~~~~~~~~~~~

label("$O$",pO,S);
draw(d1^^d2);

for (int i=n1min; i <= n1max; ++i)
  {
   dot(locate((i,0)));write(i);
  }
for (int i=n2min; i <= n2max; ++i)
  {
   dot(locate((0,i)));
  }

dot("$A$",pA,S);
dot("$B$",pB,S);
dot("$C$",pC,NW);
dot("$D$",pD,NW);

shipout(bbox(xmargin = 1mm,invisible));
Asymptote - Figure 0024: fig_na02_060708_droite_graduee.asy
(Code compilé avec Asymptote version 1.95svn)
largeur320 Figure fig_na02_060708_droite_graduee 
// La même figure que la précédente
// mais en utilisant l'instruction **sequence**
// Rappel d'un extrait de la documentation officielle :
/*
   int[] sequence(int n)
   if n >= 1 returns the array {0,1,...,n-1} (otherwise returns a null array);
*/
/*   
   int[] sequence(int n, int m)
   if m >= n returns an array {n,n+1,...,m} (otherwise returns a null array);
*/
/*
   T[] sequence(T f(int), int n)
   if n >= 1 returns the sequence {f_i :i=0,1,...n-1} given a function T f(int)
   and integer int n (otherwise returns a null array);
*/
// import geometry_dev; // extension devenue l'extension geometry officielle
import geometry;        // le 12/05/09, dans la version 1.71 d'asymptote. :-))

unitsize(1cm);

// ~~~~~~ DEFINITIONS ~~~~~~~~~~~~~~~~~~~~~~

pair pO=(0,0), pI=(1,0), pJ=rotate(45,pO)*pI;
line d1 = line(pO,pI);
line d2 = line(pO,pJ);
currentcoordsys = cartesiansystem(pO,i=pI,j=pJ);
int n1min=-2, n1max=5, n2min=-3, n2max=6;
point pA=(2,0), pB=(4,0), pC=(0,3), pD=(0,5);

// ~~~~~~ CONSTRUCTIONS ~~~~~~~~~~~~~~~~~~~~~~

label("$O$",pO,S);
draw(d1^^d2);

point f(int i){return locate((i+n1min,0));};
point[] pM1=sequence(f,n2max-n2min+1);
dot(pM1);

point g(int i){return locate((0,i+n2min));};
point[] pM2=sequence(g,n2max-n2min+1);
dot(pM2);

dot("$A$",pA,S); dot("$B$",pB,S);
dot("$C$",pC,NW); dot("$D$",pD,NW);

shipout(bbox(xmargin = 1mm,invisible));
Asymptote - Figure 0025: fig_pa01_010808_path.asy
(Code compilé avec Asymptote version 1.95svn)
largeur320 Figure fig_pa01_010808_path 
size(7.5cm,0);

path ligne=(-3,1)..(-1,2)..(4,0);

draw(ligne,blue);
dot(ligne,red);

shipout(bbox(3mm,white));
Asymptote - Figure 0026: fig_pa02_010808_path.asy
(Code compilé avec Asymptote version 1.95svn)
largeur320 Figure fig_pa02_010808_path 
size(7.5cm,0);

path ligne=(-3,1){right}..(-1,2)..(4,0);

draw(ligne,blue);
dot(ligne,red);

shipout(bbox(3mm,white));
Asymptote - Figure 0027: fig_pa03_010808_path.asy
(Code compilé avec Asymptote version 1.95svn)
largeur320 Figure fig_pa03_010808_path 
size(7.5cm,0);

path ligne=(-3,1)..{dir(-45)}(-1,2)..{right}(4,0);

draw(ligne,blue);
dot(ligne,red);

shipout(bbox(3mm,white));
Asymptote - Figure 0028: fig_pa04_010808_path.asy
(Code compilé avec Asymptote version 1.95svn)
largeur320 Figure fig_pa04_010808_path 
size(7.5cm,0);

path ligne=(-3,1)..{dir(45)}(-1,2){dir(-45)}..(4,0);

draw(ligne,blue);
dot(ligne,red);

shipout(bbox(3mm,white));
Asymptote - Figure 0029: fig_pb01_291009_path_Bezier.asy
(Code compilé avec Asymptote version 1.95svn)
largeur320 Figure fig_pb01_291009_path_Bezier 
unitsize(1cm);

pair z0=(0,0), z1=(7,0),
     c0=(1,2), c1=(5,3);

// Courbe (spline) de Bézier ...
// ... cubique (définie par 4 points).
path CourbeBezier = z0 .. controls c0 and c1 .. z1;
// Pour info : la forme paramétrique de la courbe est 
// z(t) = z0 (1-t)^3 + 3 c0 t(1-t)^2 + 3 c1 t^2(1-t) + z1 t^3
// avec t compris entre 0 et 1.

draw(CourbeBezier,2bp+blue);

path lignebrisee = z0 -- c0 -- c1 -- z1;
draw(lignebrisee,dashed); // en pointillés...
dot(lignebrisee,5bp+red); // ... et les points en rouge.

// Pour finir, on ajoute le nom des points.
label("$z_0$",z0,S);
label("$z_1$",z1,S);
label("$c_0$",c0,N);
label("$c_1$",c1,N);

shipout(bbox(3mm,white));
Asymptote - Figure 0030: fig_pb02_291009_path_Bezier.asy
(Code compilé avec Asymptote version 1.95svn)
largeur320 Figure fig_pb02_291009_path_Bezier 
// La figure précédente avec cette fois c1 confondu avec c0.

unitsize(1cm);

pair z0=(0,0), z1=(7,0), c=(1,2);

// Courbe (spline) de Bézier (cubique), 
// dans le cas où les deux points de contrôle sont confondus.
path CourbeBezier = z0 .. controls c .. z1;
// Pour info : la forme paramétrique de la courbe est 
// z(t) = z0 (1-t)^3 + 3 c t(1-t) + z1 t^3
// avec t compris entre 0 et 1.

draw(CourbeBezier,2bp+blue);

path lignebrisee = z0 -- c -- z1;
draw(lignebrisee,dashed); // en pointillés...
dot(lignebrisee,5bp+red); // ... et les points en rouge.

// Pour finir, on ajoute le nom des points.
label("$z_0$",z0,S);
label("$z_1$",z1,S);
label("$c$",c,N);

shipout(bbox(3mm,white));
Asymptote - Figure 0031: fig_pb03_291009_path_Bezier.asy
(Code compilé avec Asymptote version 1.95svn)
largeur320 Figure fig_pb03_291009_path_Bezier 
unitsize(1cm);

pair z0=(0,0), z1=(7,0),
     c0=(1,3), c1=(5,5);
         
// On déduit du quadruplet de points précédents (z0, c0, c1, z1)
// (par construction de 6 milieux) le point z2 sur la courbe de bézier.
// En procédant de même pour les quadruplets (z0, m0, m3, z2)
// et (z2, m4, m2, z1), on obtiendrait deux nouveaux points de la courbe,
// et c'est en continuant ainsi, par récursivité, que la courbe est construite.

pair m0=(z0+c0)/2,
         m1=(c0+c1)/2,
         m2=(c1+z1)/2,
         m3=(m0+m1)/2,
         m4=(m1+m2)/2,
         z2=(m3+m4)/2;   

// Courbe (spline) de Bézier cubique (définie par 4 points).
path CourbeBezier = z0 .. controls c0 and c1 .. z1;
draw(CourbeBezier,2bp+blue);

// Les traits et points de construction
path lignebrisee = z0 -- c0 -- c1 -- z1;
draw(lignebrisee^^m0--m1--m2^^m3--m4,dashed);
dot(lignebrisee^^m0--m1--m2^^m3--m4^^z2,5bp+red);

// Pour finir, on ajoute le nom des points.
label("$z_0$",z0,S); label("$z_1$",z1,S);
label("$c_0$",c0,N); label("$c_1$",c1,N);
label("$m_0$",m0,NW); label("$m_1$",m1,N);
label("$m_2$",m2,NE); label("$m_3$",m3,N);
label("$m_4$",m4,N); label("$z_2$",z2,N);

shipout(bbox(3mm,white));
Asymptote - Figure 0032: fig_pb04_291009_path_Bezier.asy
(Code compilé avec Asymptote version 1.95svn)
largeur320 Figure fig_pb04_291009_path_Bezier 
// Le même exemple que celui ci-dessus,
// avec des instructions de l'extension geometry.

import geometry;
unitsize(1cm);

point z0=(0,0), c0=(1,3), c1=(5,5), z1=(7,0);
segment z0c0=segment(z0,c0), c0c1=segment(c0,c1), c1z1=segment(c1,z1);
point m0=midpoint(z0c0), m1=midpoint(c0c1), m2=midpoint(c1z1);
segment m0m1=segment(m0,m1), m1m2=segment(m1,m2);
point m3=midpoint(m0m1), m4=midpoint(m1m2);
segment m3m4=segment(m3,m4);
point z2=midpoint(m3m4);

// Courbe (spline) de Bézier cubique (définie par 4 points).
path CourbeBezier = z0 .. controls c0 and c1 .. z1;
draw(CourbeBezier,2bp+blue);

// Les traits de construction.
draw(z0c0^^c0c1^^c1z1^^m0m1^^m1m2^^m3m4,dashed);

// Pour finir, on place les points en les étiquetant.
dot("$z_0$",z0,S,red); dot("$z_1$",z1,S,red);
dot("$c_0$",c0,N,green); dot("$c_1$",c1,N,green);
dot("$m_0$",m0,NW); dot("$m_1$",m1,N);
dot("$m_2$",m2,NE); dot("$m_3$",m3,N);
dot("$m_4$",m4,N); dot("$z_2$",z2,N,purple);

shipout(bbox(3mm,white));
Asymptote - Figure 0033: fig_pm01_271011_path_min_max.asy
(Code compilé avec Asymptote version 2.14svn)
largeur320 Figure fig_pm01_271011_path_min_max 
size(8cm);
// Pour matérialiser le repère :
draw((1,0)--(0,0)--(0,1),Arrows());

// Définition d'un chemin (path) :
path p=(0,0)..(2,0)..(2,1)..(0,2)..(-1.5,1.5)..(-0.5,1.5)..cycle;

// Tracé de p et placement des points le définissant.
draw("p",p,blue);
dot(p,3bp+red);
// Numérotation des points définissant p.
for(int k; k<length(p); ++k) label(string(k),point(p,k),unit(accel(p,k)));

// Placement des points : min(p) et max(p)
dot("min(p)",min(p),S,2bp+blue);
dot("max(p)",max(p),N,2bp+blue);

// Placement des points "extrêmes" de p 
dot("A",point(p,mintimes(p)[0]),W,2bp+green);
dot("B",point(p,mintimes(p)[1]),S,2bp+green);
dot("C",point(p,maxtimes(p)[0]),E,2bp+green);
dot("D",point(p,maxtimes(p)[1]),N,2bp+green);
// Affichage des valeurs de "time" des 4 points précédents.
label("A : mintimes(p)[0]="+string(mintimes(p)[0]),truepoint(S),S);
label("B : mintimes(p)[1]="+string(mintimes(p)[1]),truepoint(S),S);
label("C : maxtimes(p)[0]="+string(maxtimes(p)[0]),truepoint(S),S);
label("D : maxtimes(p)[1]="+string(maxtimes(p)[1]),truepoint(S),S);
Asymptote - Figure 0034: fig_pt01_271011_path_times.asy
(Code compilé avec Asymptote version 2.14svn)
largeur320 Figure fig_pt01_271011_path_times 
// La fonction times(path p, real x=a) bien pratique pour connaitre le 
// "time" des points d'intersection de p avec la droite d'équation x=a.

import geometry;
size(8cm,0);
// Pour matérialiser le repère :
draw((1,0)--(0,0)--(0,1),Arrows());
// Tracé d'un chemin(path) p et placement des points le définissant.
path p=(-.5,0)..(2,0)..(2,1)..(0,2)..(-1.5,1)..(-0.5,1.5)..cycle;
draw("p",p);
dot(p,2bp+black);
for(int k; k<length(p); ++k) label(string(k),point(p,k),unit(accel(p,k)));

real a=-1, b=-.5, c=2;
real[] ta=times(p,a),
       tb=times(p,b),
       tc=times(p,c);
for(int k=0; k<ta.length; ++k) dot(point(p,ta[k]),3bp+red);
for(int k=0; k<tb.length; ++k) dot(point(p,tb[k]),3bp+blue);
for(int k=0; k<tc.length; ++k) dot(point(p,tc[k]),3bp+green);
draw(Label(format("$x=%f$",a),BeginPoint,S),line(1,0,-a),dashed+red);
draw(Label(format("$x=%f$",b),EndPoint,N),line(1,0,-b),dashed+blue);
draw(Label(format("$x=%f$",c),BeginPoint,S),line(1,0,-c),dashed+green);

addMargins(0,1cm);
Asymptote - Figure 0035: fig_pt02_271011_path_times.asy
(Code compilé avec Asymptote version 2.14svn)
largeur320 Figure fig_pt02_271011_path_times 
// La fonction times(path p, pair z) bien pratique pour connaitre le 
// "time" des points d'intersection de p avec la droite horizontale
// passant par le point z.

import geometry;
size(8cm,0);
// Pour matérialiser le repère :
draw((1,0)--(0,0)--(0,1),Arrows());
// Tracé d'un chemin(path) p et placement des points le définissant.
path p=(-.5,0)..(2,0)..(2,1)..(0,2)..(-1.5,1)..(-0.5,1.5)..cycle;
draw("p",p);
dot(p,2bp+black);
for(int k; k<length(p); ++k) label(string(k),point(p,k),unit(accel(p,k)));

pair pA=(0,-1), pB=(0,0.5), pC=(0,1.3);
real[] ta=times(p,pA),
       tb=times(p,pB),
       tc=times(p,pC);
for(int k=0; k<ta.length; ++k) dot(point(p,ta[k]),3bp+red);
for(int k=0; k<tb.length; ++k) dot(point(p,tb[k]),3bp+blue);
for(int k=0; k<tc.length; ++k) dot(point(p,tc[k]),3bp+green);
draw(Label(format("$y=%f$",pA.y),BeginPoint,SW),line(0,1,-pA.y),dashed+red);
draw(Label(format("$y=%f$",pB.y),EndPoint,NE),line(0,1,-pB.y),dashed+blue);
draw(Label(format("$y=%f$",pC.y),BeginPoint,NW),line(0,1,-pC.y),dashed+green);

addMargins(.5cm,.2cm);
Asymptote - Figure 0036: fig_sa01_051111_bspline_accel.asy
(Code compilé avec Asymptote version 2.14svn)
largeur320 Figure fig_sa01_051111_bspline_accel 
/* Fonction accel
   Syntaxe 1 : pair accel(path p, int t, int sign=0);
               If sign < 0, return the acceleration of the incoming path p at node t ; 
               if sign > 0, return the acceleration of the outgoing path. 
               if sign=0, the mean of these two accelerations is returned.
               
   Syntaxe 2 : pair accel(path p, real t);
               returns the acceleration of the path p at the point t.
*/
import geometry;
size(7.5cm,0);
path p=(-5,0)..(10,0)..(10,10)..(0,20)..(-10,20)..(-5,15)..cycle;
draw("p",p); dot(p,2bp+black);
pair po, pa;
for(real k=0; k<length(p); k+=.05)
{
  po=point(p,k);
  pa = po+(accel(p,k))/6;
  draw(po--pa,red);
}
void acceleration(path p, int k, real t){
     pair z0=point(p,k),
          c0=postcontrol(p,k),
          z1=point(p,k+1),
          c1=precontrol(p,k+1),
          m0=(1-t)*z0+t*c0,
          m1=(1-t)*c0+t*c1,
          m2=(1-t)*c1+t*z1,
          m3=(1-t)*m0+t*m1,
          m4=(1-t)*m1+t*m2,
          z2=(1-t)*m3+t*m4;
     path CourbeBezier = z0 .. controls c0 and c1 .. z1;
     draw(CourbeBezier,1bp+blue);
     path lignebrisee = z0 -- c0 -- c1 -- z1;
     draw(lignebrisee^^m0--m1--m2^^m3--m4,linetype("4 4"));
     dot(z0^^z1^^z2,blue); dot(c0^^c1,gray);
     dot(m0--m1--m2^^m3--m4,green);
     draw(z2--(z2+accel(CourbeBezier,t)/6),.8bp+.5green,Arrow());
     write((precontrol(p,k)+postcontrol(p,k))/2-point(p,k));
}
acceleration(p,1,.75);
acceleration(p,3,.75);
acceleration(p,5,.75);
addMargins(2mm,2mm);
Asymptote - Figure 0037: fig_si01_160812_size_length.asy
(Code compilé avec Asymptote version 2.14svn)
largeur320 Figure fig_si01_160812_size_length 
// Ne pas confondre size, length et arclength !
size(7.5cm,0);

path chemin=(-3,1)..(-1,2)..(4,0)..(5,3);

draw(chemin,blue,dot);
label(format("size(chemin) = %i",size(chemin)),truepoint(S),S);
label(format("length(chemin) = %i",length(chemin)),truepoint(S),S);
label(format("arclength(chemin) = %f",arclength(chemin)),truepoint(S),S);

shipout(bbox(3mm,white));
Asymptote - Figure 0038: fig_ta00_211112_time.asy
(Code compilé avec Asymptote version 2.22svn-r5538)
largeur320 Figure fig_ta00_211112_time 
/* Exemple pour comprendre ce que l'on appelle le time 
   d'un point d'un chemin.
*/
usepackage("xcolor");
size(8cm,0);
path chemin=(-3,1)..(-1,2)..(4,0)..(5,3);

draw(chemin,blue,dot);
for(int k=0; k<size(chemin); ++k) label(string(k),point(chemin,k),N);

dot("$1.3$",point(chemin,1.3),S,red);

label(minipage("\small Exemple d'un chemin d\'efini par 4 noeuds.\\
                Chaque chiffre noir est le \emph{time} du noeud.
                \textcolor{red}{\tt point(chemin,1.3)} est le point de \emph{time} $1,3$.\\",
                7.6cm),truepoint(S),S);                
                
shipout(bbox(1mm,white));
Asymptote - Figure 0039: fig_ta01_010808_arctime.asy
(Code compilé avec Asymptote version 2.22svn-r5538)
largeur320 Figure fig_ta01_010808_arctime 
// EXEMPLE COMPLETEMENT REVU - POUR SIMPLIFICATION - LE 21/11/12

// Trois fonctions à connaitre : arctime, dirtime, reltime.
// Illustrons dans cet exemple l'utilisation de arctime et arcpoint.
 
/* real arctime(path p, real L);
        renvoie le "time" du point à la distance curviligne L du noeud 0 sur le chemin p.
        
   pair arcpoint(path p, real L);
        renvoie le couple de coordonnées du point à la distance curviligne L du noeud 0 sur le chemin p.
*/
usepackage("xcolor");
import markers;
import geometry;
show(defaultcoordsys);
size(8cm,0);

path ligne=(-3,5.5){dir(60)}..(-.5,6)..(3.5,-1.5)..{dir(80)}(5,1);
     
draw(ligne,blue,dot);
for(int k=0; k<size(ligne); ++k) label(string(k),point(ligne,k),N);

// Subdivisons le debut de la ligne, sur une longueur 10, en 10...
// ... en mettant donc 11 points rouges espacés de 1.
draw(subpath(ligne,0,arctime(ligne,10)),
     nullpen, // << pour ne pas tracer la restriction de la ligne
     StickIntervalMarker(i=10,n=2,size=1mm,space=.5mm,dotframe(1.9bp+red))
     );
/* arctime(ligne,10) a permis d'avoir le "time" du point qui est à une distance 
   curviligne 10 du début de la ligne... qui était attendu par la fonction subpath.
*/
draw(Label(minipage("\footnotesize\textcolor{red}{\tt arcpoint(ligne,10)}\color{purple}\\
                     (point situ\'e à une distance curviligne 10 du noeud 0)
                     dont le \emph{time} est donn\'e\\
                     par \textcolor{red}{\tt arctime(ligne,10)}.\\
                     {\tt arctime(ligne,10)}$\approx 1,71$",4.2cm),position=BeginPoint),
                     (2.2,2.5)--arcpoint(ligne,10),Arrow); 

// write(arctime(ligne,10)); // Affichage en console : 1.70681592073236
                     
shipout(bbox(1mm,white));
Asymptote - Figure 0040: fig_tb01_010808_dirtime.asy
(Code compilé avec Asymptote version 2.22svn-r5538)
largeur320 Figure fig_tb01_010808_dirtime 
// EXEMPLE COMPLETEMENT REVU - POUR SIMPLIFICATION - LE 21/11/12

// Trois fonctions à connaitre : arctime, dirtime, reltime.
// Illustrons dans cet exemple l'utilisation de dirtime.
 
/* real dirtime(path p, pair z);;
        renvoie le "time" du premier point de p en lequel 
        la tangente est dirigée par le vecteur directeur choisi.
*/
size(8cm,0);

path ligne=(-3,5.5){dir(60)}..(-.5,6)..(3.5,-1.5)..{dir(80)}(5,1);
draw(ligne,blue,dot);

// Des vecteurs directeurs
pair v[]= {(2,-10),(2,-4),(2,-3),(2,-2),(2,-1),(2,0),
           (2,1),(2,2),(2,3),(2,4),(2,8)};
int   n = v.length;

for(int k=0; k<n; ++k)
{
    real dt=dirtime(ligne,v[k]);
    dot(point(ligne,dt),1.9bp+red);
    draw(Label("("+string(v[k].x)+";"+string(v[k].y)+")",EndPoint),
         point(ligne,dt)--point(ligne,dt)+v[k],
         red,Arrow);
}
shipout(bbox(1mm,white));
Asymptote - Figure 0041: fig_tc01_010808_reltime.asy
(Code compilé avec Asymptote version 2.22svn-r5538)
largeur320 Figure fig_tc01_010808_reltime 
// EXEMPLE COMPLETEMENT REVU - POUR SIMPLIFICATION - LE 21/11/12

// Trois fonctions à connaitre : arctime, dirtime, reltime.
// Illustrons dans cet exemple l'utilisation de reltime et relpoint.
 
/* real reltime(path p, real l);
        renvoie le "time" du point de p situé à une distance 
        relative l (comprise entre 0 et 1) du noeud 0.
        
   pair relpoint(path p, real l);
        renvoie le couple de coordonnées du point de p situé à une distance 
        relative l (comprise entre 0 et 1) du noeud 0.
*/
usepackage("xcolor");
import markers;
size(8cm,0);

path ligne=(-3,5.5){dir(60)}..(-.5,6)..(3.5,-1.5)..{dir(80)}(5,1);
     
draw(ligne,blue,dot);
for(int k=0; k<size(ligne); ++k) label(string(k),point(ligne,k),N);

// Subdivisons, en 7, les premiers 70\% de la ligne... 
// ... en mettant donc 8 points rouges \'egalement espac\'es.
draw(subpath(ligne,0,reltime(ligne,0.7)),
     nullpen, // << pour ne pas tracer la restriction de la ligne
     StickIntervalMarker(i=7,n=3,size=1mm,space=.5mm,dotframe(1.9bp+red))
     );
// reltime(ligne,0.7) a permis d'avoir le "time" du point qui est à 70% de la longueur 
// de la ligne à partir du noeud 0... qui était attendu par la fonction subpath.

draw(Label(minipage("\footnotesize\textcolor{red}{\tt relpoint(ligne,0.7)}\color{purple}\\
                     (point situ\'e à une distance relative de 70\% du noeud 0)\\
                     dont le \emph{time} est donn\'e\\
                     par \textcolor{red}{\tt reltime(ligne,0.7)}.\\
                     {\tt reltime(ligne,0.7)}$\approx 1,85$",4.4cm),position=BeginPoint),
                     (2.7,2.7)--relpoint(ligne,0.7),Arrow); 

write(reltime(ligne,0.7)); // Affichage en console : 1.84697282506223
                     
shipout(bbox(1mm,white));
Page Asymptote du site référent / Page d'accueil de la galerie / FORUM ASYMPTOTE

Dernière modification le Thu Nov 22 00:45:29 CET 2012 par G.Marris       Valide XHTML