Page Asymptote du site référent / Page d'accueil de la galerie / FORUM ASYMPTOTE
INTERSECTIONS (20)
Liste des figures
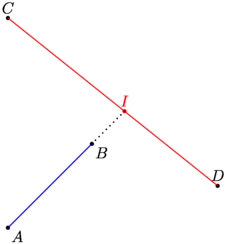
Figure fig_aa01_190208_fonction_extension
figure 0001
Figure fig_ba01_240208_fonction_intersectionpoint
figure 0002
Figure fig_ba01_240708_fonction_intersectionpoint
figure 0003
Figure fig_ba02_240208_fonction_intersectionpoint
figure 0004
Figure fig_ba03_240708_fonction_intersectionpoint
figure 0005
Figure fig_ba04_240708_fonction_intersectionpoint
figure 0006
Figure fig_ca01_240208_fonction_intersectionpoints
figure 0007
Figure fig_ca02_271209_fonction_intersectionpoints
figure 0008
Figure fig_ca03_271209_fonction_intersectionpoints
figure 0009
Figure fig_ca04_271209_fonction_intersectionpoints
figure 0010
Figure fig_da01_081109_fonction_intersectionpoints
figure 0011
Figure fig_da02_081109_fonction_intersectionpoints
figure 0012
Figure fig_fa01_240708_firstcut_lastcut
figure 0013
Figure fig_fa02_240708_firstcut_lastcut
figure 0014
Figure fig_fa03_240708_firstcut_lastcut
figure 0015
Figure fig_fa04_240708_firstcut_lastcut
figure 0016
Figure fig_ia01_260708_fonction_intersect
figure 0017
Figure fig_ia02_260708_fonction_intersect
figure 0018
Figure fig_pt01_271011_path_times
figure 0019
Figure fig_pt02_271011_path_times
figure 0020
Asymptote - Figure 0001: fig_aa01_190208_fonction_extension.asy
(Code compilé avec Asymptote version 2.14svn)
largeur320 Figure fig_aa01_190208_fonction_extension 
size(6cm,0);
import math;

// Placement de 4 points
pair A=(0,0),B=(2,2),C=(0,5),D=(5,1);
dot("$A$",A,SE);
dot("$B$",B,SE);
dot("$C$",C,N);
dot("$D$",D,N);

// Tracé de [AB] et [CD]
draw(A--B,blue);
draw(C--D,red);

// Construction du point
// d'intersection de (AB) et (CD)
pair pI=extension(A,B,C,D);
dot("$I$",pI,N,red);
draw(B--pI,1pt+dotted);
Asymptote - Figure 0002: fig_ba01_240208_fonction_intersectionpoint.asy
(Code compilé avec Asymptote version 1.95svn)
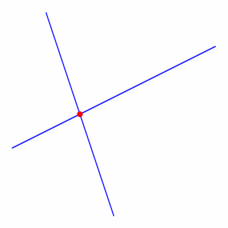
largeur320 Figure fig_ba01_240208_fonction_intersectionpoint 
size(6cm,0);

path segm1=(-1,-1)--(5,2),
    segm2=(0,3)--(2,-3);
draw(segm1^^segm2,blue);

dot(intersectionpoint(segm1,segm2),4bp+red);

shipout(bbox(3mm,white));
Asymptote - Figure 0003: fig_ba01_240708_fonction_intersectionpoint.asy
(Code compilé avec Asymptote version 1.95svn)
largeur320 Figure fig_ba01_240708_fonction_intersectionpoint 
size(7.5cm,0);
// ~~~~~~~~~ DEFINITIONS ~~~~~~~~~
path droite=(-5,5)--(-1,1),
     cercle=circle((1,0),3);
pair pA=intersectionpoint(droite,cercle);
// ~~~~~~~~~ CONSTRUCTIONS ~~~~~~~~~
draw(droite,blue);
draw(cercle,orange);
dot("$A$",pA,2W,4bp+brown);

shipout(bbox(3mm,white));
Asymptote - Figure 0004: fig_ba02_240208_fonction_intersectionpoint.asy
(Code compilé avec Asymptote version 1.95svn)
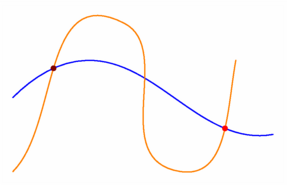
largeur320 Figure fig_ba02_240208_fonction_intersectionpoint 
// Si dans l'exemple précédent la fonction **intersectionpoints** 
// renvoie un tableau des points d'intersection, 
// dans cet exemple la fonction **intersectionpoints** (sans 's' !)
// renvoie le premier point d'intersection rencontré.
size(7.5cm,0);
defaultpen(.8bp);

path ligne1=(-3,1){dir(45)}..(-1,2)..{dir(10)}(4,0),
     ligne2=(-3,-1){dir(45)}..(0,3)..(1.5,-1)..{dir(80)}(3,2);
draw(ligne1,blue);
draw(ligne2,orange);
// 
dot(intersectionpoint(ligne1,ligne2),4bp+brown);
dot(intersectionpoint(reverse(ligne1),ligne2),4bp+red);

shipout(bbox(3mm,white));
Asymptote - Figure 0005: fig_ba03_240708_fonction_intersectionpoint.asy
(Code compilé avec Asymptote version 1.95svn)
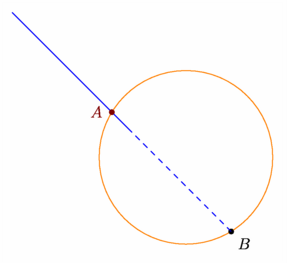
largeur320 Figure fig_ba03_240708_fonction_intersectionpoint 
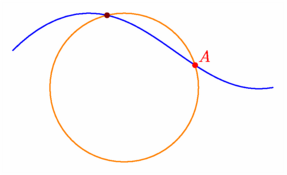
size(7.5cm,0);
// ~~~~~~~~~ DEFINITIONS ~~~~~~~~~
pair p1=(-5,5), p2=(-1,1);
path droite=p1--p2,
     cercle=circle((1,0),3);
pair pA=intersectionpoint(droite,cercle),
     pB=intersectionpoint(p2--interp(p1,p2,2),cercle);
// ~~~~~~~~~ CONSTRUCTIONS ~~~~~~~~~
draw(droite,blue);
draw(cercle,orange);
dot("$A$",pA,2W,4bp+brown);
dot("$B$",pB,2SE,4bp+black);
draw(p2--pB,dashed+blue);

shipout(bbox(3mm,white));
Asymptote - Figure 0006: fig_ba04_240708_fonction_intersectionpoint.asy
(Code compilé avec Asymptote version 1.95svn)
largeur320 Figure fig_ba04_240708_fonction_intersectionpoint 
size(7.5cm,0);
defaultpen(.8bp);
// ~~~~~~~~~ DEFINITIONS ~~~~~~~~~
path ligne=(-3,1){dir(45)}..(-1,2)..{dir(10)}(4,0),
     cercle=scale(2)*unitcircle;
pair point1=intersectionpoint(ligne,cercle),
     point2=intersectionpoint(reverse(ligne),cercle);
// ~~~~~~~~~ CONSTRUCTIONS ~~~~~~~~~
draw(ligne,blue);
draw(cercle,orange);
dot(point1,4bp+brown);
dot("$A$",point2,NE,4bp+red);

shipout(bbox(3mm,white));
Asymptote - Figure 0007: fig_ca01_240208_fonction_intersectionpoints.asy
(Code compilé avec Asymptote version 1.95svn)
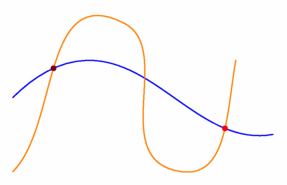
largeur320 Figure fig_ca01_240208_fonction_intersectionpoints 
size(7.5cm,0);
defaultpen(.8bp);

path ligne1=(-3,1){dir(45)}..(-1,2)..{dir(10)}(4,0),
    ligne2=(-3,-1){dir(45)}..(0,3)..(1.5,-1)..{dir(80)}(3,2);
draw(ligne1,blue);
draw(ligne2,orange);
// intersectionpoints renvoie un tableau des points d'intersection
pair [] tabpts=intersectionpoints(ligne1,ligne2);
// le premier point est indicé 0, le deuxième 1, etc...
dot(tabpts[0],4bp+brown);
dot(tabpts[2],4bp+red);

shipout(bbox(3mm,white));
Asymptote - Figure 0008: fig_ca02_271209_fonction_intersectionpoints.asy
(Code compilé avec Asymptote version 1.95svn)
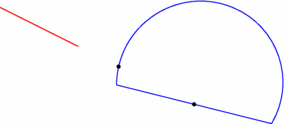
largeur320 Figure fig_ca02_271209_fonction_intersectionpoints 
size(7.5cm,0);

pair pA=(-3,2), pB=(-1,1);

path segm=pA--pB,
     chemin=(0,0)--(4,-1)..(3,2)..cycle;

draw(chemin,blue);
draw(segm,red);

dot(intersectionpoints(pA--interp(pA,pB,3),chemin));
Asymptote - Figure 0009: fig_ca03_271209_fonction_intersectionpoints.asy
(Code compilé avec Asymptote version 1.95svn)
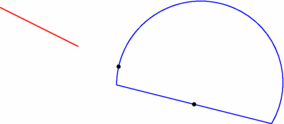
largeur320 Figure fig_ca03_271209_fonction_intersectionpoints 
size(7.5cm,0);
import geometry;

pair pA=(-3,2), pB=(-1,1);

path segm=pA--pB,
     chemin=(0,0)--(4,-1)..(3,2)..cycle;

draw(chemin,blue);
draw(segm,red);

dot(intersectionpoints(line(pA,pB),chemin));
Asymptote - Figure 0010: fig_ca04_271209_fonction_intersectionpoints.asy
(Code compilé avec Asymptote version 1.95svn)
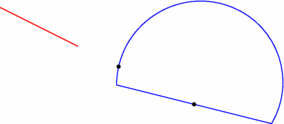
largeur320 Figure fig_ca04_271209_fonction_intersectionpoints 
size(7.5cm,0);
import geometry;

point pA=(-3,2), pB=(-1,1);

path chemin=(0,0)--(4,-1)..(3,2)..cycle;

draw(chemin,blue);
draw(segment(pA,pB),red);

dot(intersectionpoints(line(pA,pB),chemin));
Asymptote - Figure 0011: fig_da01_081109_fonction_intersectionpoints.asy
(Code compilé avec Asymptote version 1.95svn)
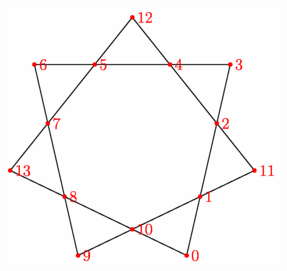
largeur320 Figure fig_da01_081109_fonction_intersectionpoints 
// Intersection d'un "path" avec lui-même.
size(7.5cm,0);

// ~~~~~~~~~ DEFINITIONS ~~~~~~~~~
path chemin;
for (int i=0; i<=7; ++i) chemin=chemin--point(polygon(7),2*i);
pair[] p = intersectionpoints(chemin,chemin);

// ~~~~~~~~~ CONSTRUCTIONS ~~~~~~~~~
draw(chemin);
for (int k=0; k<p.length; ++k) dot(format("%i",k),p[k],red);

shipout(bbox(2mm,white));
Asymptote - Figure 0012: fig_da02_081109_fonction_intersectionpoints.asy
(Code compilé avec Asymptote version 1.95svn)
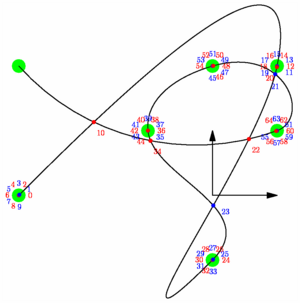
largeur320 Figure fig_da02_081109_fonction_intersectionpoints 
// Bizarre... exemple à revoir !

// Intersection d'un "path" avec lui-même.
size(7.9cm,0);

// ~~~~~~~~~ DEFINITIONS ~~~~~~~~~
path chemin=(-3,0){dir(45)}..(1,2)..{dir(45)}(0,-1)
            ..(-1,1)..(0,2)..(1,1){dir(-160)}..(-3,2);
pair[] p = intersectionpoints(chemin,chemin);
pen[] stylo={red,blue};
// ~~~~~~~~~ CONSTRUCTIONS ~~~~~~~~~
draw((0,1)--(0,0)--(1,0),Arrows);
dot(chemin,10bp+green);
draw(chemin);
for (int k=0; k<p.length; ++k) 
    dot(scale(.5)*format("%i",k),p[k],2*dir(k*30),stylo[k%2]);

shipout(bbox(1mm,white));

// Bizarre... exemple à revoir !
Asymptote - Figure 0013: fig_fa01_240708_firstcut_lastcut.asy
(Code compilé avec Asymptote version 1.95svn)
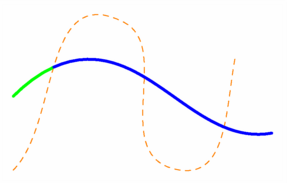
largeur320 Figure fig_fa01_240708_firstcut_lastcut 
/* dans plain_paths.asy, sont définis :
   le type : struct slice {
                path before,after;
                }
   et les fonctions :
   slice cut(path p, path knife, int n) 
   slice firstcut(path p, path knife) 
   slice lastcut(path p, path knife)
*/
size(7.5cm,0);

path ligne=(-3,1){dir(45)}..(-1,2)..{dir(10)}(4,0),
     couteau=(-3,-1){dir(45)}..(0,3)..(1.5,-1)..{dir(80)}(3,2),
     morceau1=firstcut(ligne,couteau).before,
     morceau2=firstcut(ligne,couteau).after;
// firstcut(ligne,couteau) est de type slice
// firstcut(ligne,couteau).before et firstcut(ligne,couteau).after
// sont de type path.     

draw(couteau,dashed+orange);
draw(morceau1,2bp+green); 
draw(morceau2,2bp+blue);

shipout(bbox(3mm,white));
Asymptote - Figure 0014: fig_fa02_240708_firstcut_lastcut.asy
(Code compilé avec Asymptote version 1.95svn)
largeur320 Figure fig_fa02_240708_firstcut_lastcut 
/* dans plain_paths.asy, sont définis :
   le type : struct slice {
                path before,after;
                }
   et les fonctions :
   slice cut(path p, path knife, int n) 
   slice firstcut(path p, path knife) 
   slice lastcut(path p, path knife)
*/
size(7.5cm,0);

path ligne=(-3,1){dir(45)}..(-1,2)..{dir(10)}(4,0),
     couteau=(-3,-1){dir(45)}..(0,3)..(1.5,-1)..{dir(80)}(3,2),
     morceau1=lastcut(ligne,couteau).before,
     morceau2=lastcut(ligne,couteau).after;
// firstcut(ligne,couteau) est de type slice
// firstcut(ligne,couteau).before et firstcut(ligne,couteau).after
// sont de type path.     

draw(couteau,dashed+orange);
draw(morceau1,2bp+green); 
draw(morceau2,2bp+blue);

shipout(bbox(3mm,white));
Asymptote - Figure 0015: fig_fa03_240708_firstcut_lastcut.asy
(Code compilé avec Asymptote version 1.95svn)
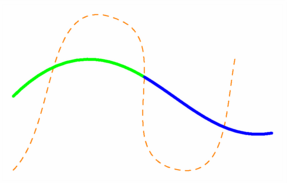
largeur320 Figure fig_fa03_240708_firstcut_lastcut 
/* dans plain_paths.asy, sont définis :
   le type : struct slice {
                path before,after;
                }
   et les fonctions :
   slice cut(path p, path knife, int n) 
   slice firstcut(path p, path knife) 
   slice lastcut(path p, path knife)
*/
size(7.5cm,0);

path ligne=(-3,1){dir(45)}..(-1,2)..{dir(10)}(4,0),
     couteau=(-3,-1){dir(45)}..(0,3)..(1.5,-1)..{dir(80)}(3,2),
     morceau1=cut(ligne,couteau,1).before,
     morceau2=cut(ligne,couteau,1).after;
// cut(ligne,couteau,n) est de type slice
// cut(ligne,couteau,n).before et cut(ligne,couteau,n).after
// sont de type path.

draw(couteau,dashed+orange);
draw(morceau1,2bp+green); 
draw(morceau2,2bp+blue);

shipout(bbox(3mm,white));
Asymptote - Figure 0016: fig_fa04_240708_firstcut_lastcut.asy
(Code compilé avec Asymptote version 1.95svn)
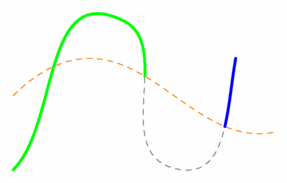
largeur320 Figure fig_fa04_240708_firstcut_lastcut 
// Et si on inverve ligne-couteau et ligne coupée...
size(7.5cm,0);

path couteau=(-3,1){dir(45)}..(-1,2)..{dir(10)}(4,0),
     ligne=(-3,-1){dir(45)}..(0,3)..(1.5,-1)..{dir(80)}(3,2),
     morceau1=cut(ligne,couteau,1).before,
     morceau2=cut(ligne,couteau,2).after;
// cut(ligne,couteau,n) est de type slice
// cut(ligne,couteau,n).before et cut(ligne,couteau,n).after
// sont de type path.

draw(couteau,dashed+orange);
draw(ligne,dashed+gray);
draw(morceau1,2bp+green); 
draw(morceau2,2bp+blue);

shipout(bbox(3mm,white));
Asymptote - Figure 0017: fig_ia01_260708_fonction_intersect.asy
(Code compilé avec Asymptote version 1.95svn)
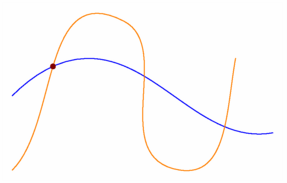
largeur320 Figure fig_ia01_260708_fonction_intersect 
/* 
real[] intersect(path p, path q, real fuzz=0);
If p and q have at least one intersection point, return a real array
of length 2 containing the times representing the respective path
times along p and q, in the sense of point(path, real), for one
such intersection point (as chosen by the algorithm described on
page 137 of The MetaFontbook). The computations are performed
to the absolute error specified by fuzz, or, if fuzz is 0, to machine
precision. If the paths do not intersect, return a real array of length

Cf. exemple suivant pour l'utilisation de
real[][] intersections(path p, path q, real fuzz=0);
*/
size(7.5cm,0);

path ligne1=(-3,1){dir(45)}..(-1,2)..{dir(10)}(4,0),
     ligne2=(-3,-1){dir(45)}..(0,3)..(1.5,-1)..{dir(80)}(3,2);
real[] parametres=intersect(ligne1,ligne2);
pair pA=point(ligne1,parametres[0]);
     
draw(ligne1,blue);
draw(ligne2,orange);
// 
dot(pA,4bp+brown);

shipout(bbox(3mm,white));
Asymptote - Figure 0018: fig_ia02_260708_fonction_intersect.asy
(Code compilé avec Asymptote version 1.95svn)
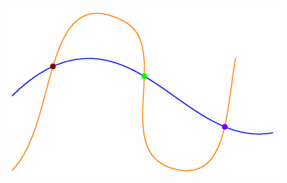
largeur320 Figure fig_ia02_260708_fonction_intersect 
/* 
real[][] intersections(path p, path q, real fuzz=0);
Return all intersection times of paths p and q as a sorted array of
real arrays of length 2 (see [sort], page 67). The computations are
performed to the absolute error specified by fuzz, or, if fuzz is 0,
to machine precision.

Cf. exemple précédent pour l'utilisation de
real[] intersect(path p, path q, real fuzz=0);
*/
size(7.5cm,0);

path ligne1=(-3,1){dir(45)}..(-1,2)..{dir(10)}(4,0),
     ligne2=(-3,-1){dir(45)}..(0,3)..(1.5,-1)..{dir(80)}(3,2);
real[][] parametres=intersections(ligne1,ligne2);
pair pA=point(ligne1,parametres[0][0]),
     pB=point(ligne1,parametres[1][0]),
     pC=point(ligne2,parametres[2][1]);
     
draw(ligne1,blue);
draw(ligne2,orange);
// 
dot(pA,4bp+brown);
dot(pB,4bp+green);
dot(pC,4bp+purple);

shipout(bbox(3mm,white));
Asymptote - Figure 0019: fig_pt01_271011_path_times.asy
(Code compilé avec Asymptote version 2.14svn)
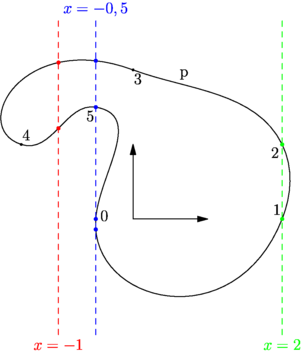
largeur320 Figure fig_pt01_271011_path_times 
// La fonction times(path p, real x=a) bien pratique pour connaitre le 
// "time" des points d'intersection de p avec la droite d'équation x=a.

import geometry;
size(8cm,0);
// Pour matérialiser le repère :
draw((1,0)--(0,0)--(0,1),Arrows());
// Tracé d'un chemin(path) p et placement des points le définissant.
path p=(-.5,0)..(2,0)..(2,1)..(0,2)..(-1.5,1)..(-0.5,1.5)..cycle;
draw("p",p);
dot(p,2bp+black);
for(int k; k<length(p); ++k) label(string(k),point(p,k),unit(accel(p,k)));

real a=-1, b=-.5, c=2;
real[] ta=times(p,a),
       tb=times(p,b),
       tc=times(p,c);
for(int k=0; k<ta.length; ++k) dot(point(p,ta[k]),3bp+red);
for(int k=0; k<tb.length; ++k) dot(point(p,tb[k]),3bp+blue);
for(int k=0; k<tc.length; ++k) dot(point(p,tc[k]),3bp+green);
draw(Label(format("$x=%f$",a),BeginPoint,S),line(1,0,-a),dashed+red);
draw(Label(format("$x=%f$",b),EndPoint,N),line(1,0,-b),dashed+blue);
draw(Label(format("$x=%f$",c),BeginPoint,S),line(1,0,-c),dashed+green);

addMargins(0,1cm);
Asymptote - Figure 0020: fig_pt02_271011_path_times.asy
(Code compilé avec Asymptote version 2.14svn)
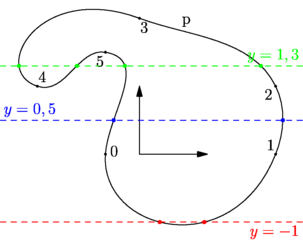
largeur320 Figure fig_pt02_271011_path_times 
// La fonction times(path p, pair z) bien pratique pour connaitre le 
// "time" des points d'intersection de p avec la droite horizontale
// passant par le point z.

import geometry;
size(8cm,0);
// Pour matérialiser le repère :
draw((1,0)--(0,0)--(0,1),Arrows());
// Tracé d'un chemin(path) p et placement des points le définissant.
path p=(-.5,0)..(2,0)..(2,1)..(0,2)..(-1.5,1)..(-0.5,1.5)..cycle;
draw("p",p);
dot(p,2bp+black);
for(int k; k<length(p); ++k) label(string(k),point(p,k),unit(accel(p,k)));

pair pA=(0,-1), pB=(0,0.5), pC=(0,1.3);
real[] ta=times(p,pA),
       tb=times(p,pB),
       tc=times(p,pC);
for(int k=0; k<ta.length; ++k) dot(point(p,ta[k]),3bp+red);
for(int k=0; k<tb.length; ++k) dot(point(p,tb[k]),3bp+blue);
for(int k=0; k<tc.length; ++k) dot(point(p,tc[k]),3bp+green);
draw(Label(format("$y=%f$",pA.y),BeginPoint,SW),line(0,1,-pA.y),dashed+red);
draw(Label(format("$y=%f$",pB.y),EndPoint,NE),line(0,1,-pB.y),dashed+blue);
draw(Label(format("$y=%f$",pC.y),BeginPoint,NW),line(0,1,-pC.y),dashed+green);

addMargins(.5cm,.2cm);
Page Asymptote du site référent / Page d'accueil de la galerie / FORUM ASYMPTOTE

Dernière modification le Fri Oct 28 12:59:22 CEST 2011 par G.Marris       Valide XHTML