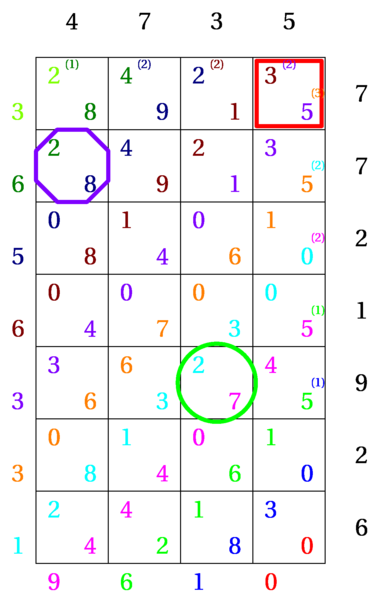
// VERSION PROVISOIRE
// 1. Des améliorations sont prévues pour la saisie des nombres.
// 2. Je n'oublie pas les traits qui manquent.

import math;
import fontsize;
usepackage("fourier");
defaultpen(fontsize(20pt));

size(10cm,0);

void jalousie(int[] a, int[] b) {
    int[][][] produit=new int[a.length][b.length][2];
    real decal=0.25;
    int[] totaldiag; for(int z=0; z<a.length+b.length; ++z) totaldiag.push(0);
    int   d=0, x, y;
    for(int j=0; j<a.length+b.length-1; ++j)
    { 
        if(j<b.length) { x=0; y=j;
                         label(string(b[y]),(1,y+1-b.length)); }
                         //draw((.5,y+1.5-b.length)--(-.5-y-2decal,.5-b.length-2decal)); }
        else { x=j-b.length+1; y=b.length-1;
               label(string(a[j+1-b.length]),(-(j+1-b.length),1)); 
        }
        while(x<a.length && y>=0) {
            produit[x][y][0]=(a[x]*b[y])%10;
            produit[x][y][1]=(int) ((a[x]*b[y]-produit[x][y][0])/10);
            totaldiag[d]+=produit[x][y][0];
            totaldiag[d+1]+=produit[x][y][1];
            label(string(produit[x][y][0]),(-x+decal,y+1-b.length-decal),Pen(d));
            label(string(produit[x][y][1]),(-x-decal,y+1-b.length+decal),Pen(d+1));
            ++x;--y;
        }
    ++d;
    }
    label(string(a[0]),(0,1));
    d=0;
    int x=0, y=-b.length, retenue;
    for(int c=0; c<a.length+b.length; ++c) {
        label(string(totaldiag[c]%10),(x-decal,y+decal),Pen(d));
        if(c< a.length+b.length-1){
            retenue=(int) ((totaldiag[c]-totaldiag[c]%10)/10);
            totaldiag[c+1]+=retenue;
            if(retenue!=0){
               real xdelta=(c<b.length-1)?.4:b.length-c-1;
               real ydelta=(c<b.length-1)?-b.length+c+2:.4;
               label(scale(.5)*format("(%i)",retenue),(xdelta,ydelta),Pen(d));
            }
        }
        if(c<a.length-1) {--x;}
        else {x=-a.length; ++y; decal=-.25;}
        ++d;
    }
    add(shift(-a.length+.5,-b.length+.5)*grid(a.length,b.length));
}

int[] a={5,3,7,4},
      b={6,2,9,1,2,7,7};

jalousie(a,b);

// Pour mettre en évidence quelques cases :
real a=.45;
path cadre1=(-a,-a)--(a,-a)--(a,a)--(-a,a)--cycle,
     cadre2=scale(1.2a)*unitcircle,
     cadre3=scale(1.2a)*polygon(8);
draw(shift(0,0)*cadre1,3bp+red);
draw(shift(-1,-4)*cadre2,3bp+green);
draw(shift(-3,-1)*cadre3,3bp+purple);

shipout(bbox(2mm,white));

frame f; 
label(f,"\textbf{2011-12}",yellow,Fill(.5yellow));
add(rotate(20)*scale(3)*f);

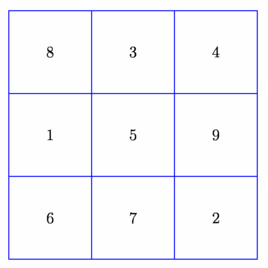
import math;
size(7cm);

void carremagique(int n){
        int i=0,j,k=1;
        int[][] carre=new int[n][n];
        for(int i=0;i<n;++i)for(int j=0;j<n;++j)carre[i][j]=0;
        j=floor(n/2);
        do {carre[i][j]=k;
            k+=1;
            if(i==0)
               i=i-1+n;
            else
               i=i-1;
            if(j==0)
               j=j-1+n;
            else
               j=j-1;
            if(carre[i][j]!=0){
                i=(i+2)%n;
                j=(j+1)%n;
            }
        } while((i!=n-1)||(j!=floor(n/2)));
        carre[i][j]=k;
        for(i=0;i<n;++i){
            for(j=0;j<n;++j){
               label(format("%i",carre[i][j]),(i,j));
            }
        }
        add(shift(-.5,-.5)*grid(n,n,blue));
}

carremagique(3);
shipout(bbox(2mm,white));

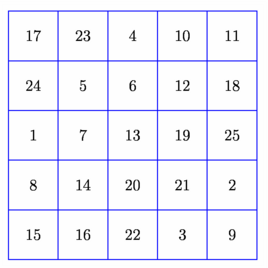
import math;
size(7cm);

void carremagique(int n){
        int i=0,j,k=1;
        int[][] carre=new int[n][n];
        for(int i=0;i<n;++i)for(int j=0;j<n;++j)carre[i][j]=0;
        j=floor(n/2);
        do {carre[i][j]=k;
            k+=1;
            if(i==0)
               i=i-1+n;
            else
               i=i-1;
            if(j==0)
               j=j-1+n;
            else
               j=j-1;
            if(carre[i][j]!=0){
                i=(i+2)%n;
                j=(j+1)%n;
            }
        } while((i!=n-1)||(j!=floor(n/2)));
        carre[i][j]=k;
        for(i=0;i<n;++i){
            for(j=0;j<n;++j){
               label(format("%i",carre[i][j]),(i,j));
            }
        }
        add(shift(-.5,-.5)*grid(n,n,blue));
}

carremagique(5);
shipout(bbox(2mm,white));

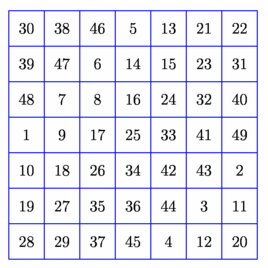
import math;
size(7cm);

void carremagique(int n){
        int i=0,j,k=1;
        int[][] carre=new int[n][n];
        for(int i=0;i<n;++i)for(int j=0;j<n;++j)carre[i][j]=0;
        j=floor(n/2);
        do {carre[i][j]=k;
            k+=1;
            if(i==0)
               i=i-1+n;
            else
               i=i-1;
            if(j==0)
               j=j-1+n;
            else
               j=j-1;
            if(carre[i][j]!=0){
                i=(i+2)%n;
                j=(j+1)%n;
            }
        } while((i!=n-1)||(j!=floor(n/2)));
        carre[i][j]=k;
        for(i=0;i<n;++i){
            for(j=0;j<n;++j){
               label(format("%i",carre[i][j]),(i,j));
            }
        }
        add(shift(-.5,-.5)*grid(n,n,blue));
}

carremagique(7);
shipout(bbox(2mm,white));

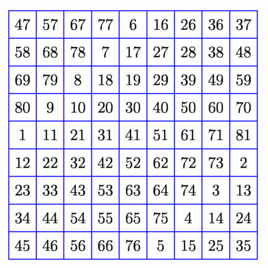
import math;
size(7cm);

void carremagique(int n){
        int i=0,j,k=1;
        int[][] carre=new int[n][n];
        for(int i=0;i<n;++i)for(int j=0;j<n;++j)carre[i][j]=0;
        j=floor(n/2);
        do {carre[i][j]=k;
            k+=1;
            if(i==0)
               i=i-1+n;
            else
               i=i-1;
            if(j==0)
               j=j-1+n;
            else
               j=j-1;
            if(carre[i][j]!=0){
                i=(i+2)%n;
                j=(j+1)%n;
            }
        } while((i!=n-1)||(j!=floor(n/2)));
        carre[i][j]=k;
        for(i=0;i<n;++i){
            for(j=0;j<n;++j){
               label(format("%i",carre[i][j]),(i,j));
            }
        }
        add(shift(-.5,-.5)*grid(n,n,blue));
}

carremagique(9);
shipout(bbox(2mm,white));

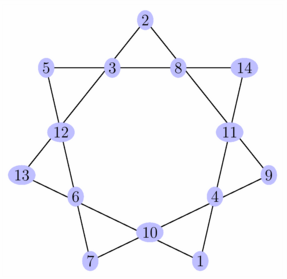
// Première solution avec positionnement approximatif des points 
// aux tiers et deux-tiers de certains segments.
// Cf. exemple fig_zb03_heptagone_magique.asy pour un meilleur positionnement.
size(7.5cm);
pen p=paleblue;
int[] nb={1,4,11,14,8,3,5,12,6,7,10,0,9,0,0,2,0,0,13,0,0,0,0};
int k=0;
picture im;
path chemin=point(polygon(7),0);
for (int i=1; i<=7; ++i) {
    chemin=chemin--point(polygon(7),2*i);
        if(nb[k]!=0) draw(im,format("%i",nb[k]),ellipse,
                             relpoint(chemin,(3i-3)/(3i)),Fill(p)); k=++k;
        if(nb[k]!=0) draw(im,format("%i",nb[k]),ellipse,
                             relpoint(chemin,(3i-2)/(3i)),Fill(p)); k=++k;
        if(nb[k]!=0) draw(im,format("%i",nb[k]),ellipse,
                             relpoint(chemin,(3i-1)/(3i)),Fill(p)); k=++k;
}       
draw(chemin);
add(im);

shipout(bbox(2mm,white));

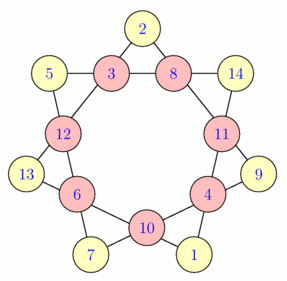
// Deuxième solution avec positionnement approximatif des points 
// aux tiers et deux-tiers de certains segments.
// Cf. exemple fig_zb03_heptagone_magique.asy pour un meilleur positionnement.
size(7.5cm);
int[] nb={1,4,11,14,8,3,5,12,6,7,10,0,9,0,0,2,0,0,13,0,0,0,0};
int k=0;
picture im;
path chemin=point(polygon(7),0);
for (int i=1; i<=7; ++i) {
    chemin=chemin--point(polygon(7),2*i);
        if(nb[k]!=0) { filldraw(im,circle(relpoint(chemin,(3i-3)/(3i)),.15),paleyellow);
                       label(im,format("%i",nb[k]),relpoint(chemin,(3i-3)/(3i)),1bp+blue);
                 } k=++k;
        if(nb[k]!=0) { filldraw(im,circle(relpoint(chemin,(3i-2)/(3i)),.15),palered);
                       label(im,format("%i",nb[k]),relpoint(chemin,(3i-2)/(3i)),1bp+blue);
                 } k=++k;
        if(nb[k]!=0) { filldraw(im,circle(relpoint(chemin,(3i-1)/(3i)),.15),palered);
                       label(im,format("%i",nb[k]),relpoint(chemin,(3i-1)/(3i)),1bp+blue);
                 } k=++k;
}       
draw(chemin);
add(im);

shipout(bbox(2mm,white));

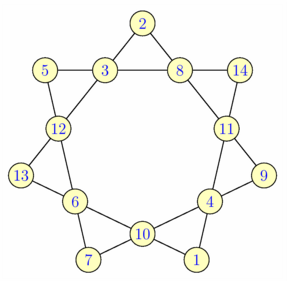
// Troisième solution : la meilleure !

size(7.5cm);
int[] nb={1,4,11,14,8,3,5,12,6,7,10,9,2,13};
int k=0;

path chemin;
for (int i=0; i<=7; ++i) chemin=chemin--point(polygon(7),2*i);
pair[] p = intersectionpoints(chemin,chemin);

draw(chemin);
for (int k=0; k<14; ++k) {
        filldraw(circle(p[k],.1),paleyellow);
        label(format("%i",nb[k]),p[k],1bp+blue);
}       
shipout(bbox(2mm,white));