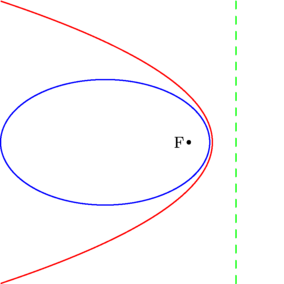
/* L'extension geometry de Philippe Ivaldi
   introduit une nouvelle structure pour les coniques :
   struct conic { real e, p, h; point F; line D; }
   - e est l'excentricité ;
   - F est un foyer et D la directrice associée ;
   - h est la distance de F à D
   - p est le paramètre, il vérifie l'égalité p=he.
   
   Une des deux principales routines 
   pour définir une conique quelconque est :
       conic conic(point F, line l, real e)
*/
// import geometry_dev; // extension devenue l'extension geometry officielle
import geometry;        // le 12/05/09, dans la version 1.71 d'asymptote. :-))

size(7.5cm,0);
point foyer=(0,0); dot("F", foyer, W);

line directrice=line((1,-1),(1,1)); 
draw(directrice,dashed+.7bp+green);

// Une ellipse lorsque 0 < e < 1
conic ell=conic(foyer,directrice,.8); 
draw(ell,.8bp+blue);

// Une parabole lorsque e = 1
conic par=conic(foyer,directrice,1); 
draw(par,.8bp+red);

draw(box((-2,-3), (2,3)), invisible);

/* L'extension geometry de Philippe Ivaldi
   introduit une nouvelle structure pour les coniques :
   struct conic { real e, p, h; point F; line D; }
   - e est l'excentricité ;
   - F est un foyer et D la directrice associée ;
   - h est la distance de F à D
   - p est le paramètre, il vérifie l'égalité p=he.
   
   Une des deux principales routines 
   pour définir une conique quelconque est :
       conic conic(point F, line l, real e)
*/
// import geometry_dev; // extension devenue l'extension geometry officielle
import geometry;        // le 12/05/09, dans la version 1.71 d'asymptote. :-))

size(7.5cm,0);
point foyer=(0,0); dot("F", foyer, W);

line directrice=line((0,2),(2,0)); 
draw(directrice,dashed+.7bp+green);

// Un cercle lorsque e = 0
conic par=conic(foyer,directrice,0); 
draw(par,.8bp+black);

// Une ellipse lorsque 0 < e < 1
conic ell=conic(foyer,directrice,.8); 
draw(ell,.8bp+blue);

// Une parabole lorsque e = 1
conic par=conic(foyer,directrice,1); 
draw(par,.8bp+red);

// Une hyperbole lorsque e > 1
conic par=conic(foyer,directrice,1.5); 
draw(par,.8bp+green);


draw(box((-3,-3), (7,7)), invisible);

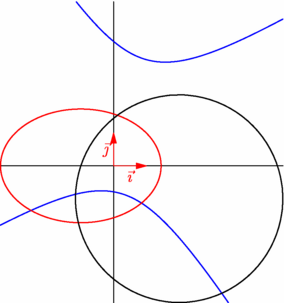
/* Une autre routine pour définir une conique est
        conic conic(bqe bqe) 
  qui retourne la conique dont une équation est représentée par bqe.
  bqe signifie 'bivariate quartic equation, c'est à la fois :
- un type dont la structure est : coordsys coordsys
                                  real[] a
  avec a tableau des 6 coefficients tels que : 
  a[0]x^2+a[1]xy+a[2]y^2+a[3]x+a[4]y+a[0]=0
- une fonction :
  bqe(coordsys R=currentcoordsys,real a,real b,real c,real d,real e,real f)
  retourne un objet de type bqe représentant l'équation 
  ax^2 + bxy + cy^2 + dx + ey + f = 0, relativement au repère R.
*/
// import geometry_dev; // extension devenue l'extension geometry officielle
import geometry;        // le 12/05/09, dans la version 1.71 d'asymptote. :-))

size(7.5cm,0);

show(currentcoordsys,dotpen=invisible);

// hyperbole d'équation x^2-xy-y^2+3y+3=0
conic c1=conic(bqe(1,-1,-1,0,3,3));
draw(c1,.8bp+blue);

// ellipse d'équation x^2+2y^2+2x-5=0
conic c2=conic(bqe(1,0,2,2,0,-5));
draw(c2,.8bp+red);

// cercle d'équation x^2+y^2-4x+2y-5=0
conic c2=conic(bqe(1,0,1,-4,2,-5));
draw(c2,.8bp+black);

draw(box((-2,-4), (5,5)), invisible);

/* bqe signifie 'bivariate quartic equation, c'est à la fois :
- un type dont la structure est : coordsys coordsys
                                  real[] a
  avec a tableau des 6 coefficients tels que : 
  a[0]x^2+a[1]xy+a[2]y^2+a[3]x+a[4]y+a[0]=0
- une fonction décrite dans l'exemple précédent.
*/
// import geometry_dev; // extension devenue l'extension geometry officielle
import geometry;        // le 12/05/09, dans la version 1.71 d'asymptote. :-))

size(7.5cm,0);

show(currentcoordsys,dotpen=invisible);

point pA=(4,0), pB=(0,2), pC=(-4,0), pD=(0,-2), pE=(3,1);
dot(pA^^pB^^pC^^pD^^pE);

conic c = conic(pA,pB,pC,pD,pE);
draw(c,.8bp+.8green);

// equation(explicit conic co)
// est une fonction qui retourne l'équation d'une conique.
// sous la forme d'un objet bqe (repère + tableau des coefficients)
bqe eq = equation(c);
string[] b={"$x^2+$","$xy+$","$y^2+$","$x+$","$y+$","=0"};
string equ="L'\'equation de la conique est :\par";
for(int k=0; k<6; ++k) equ += format("(%.3f)",eq.a[k])+b[k];
equ += "\par (coefficients \'eventuellement arrondis)";
label(minipage(equ,width=250),(0,4));

// string conictype(bqe bqe)
// est une fonction qui retourne le type d'une conique.

label("La conique est de type : "+conictype(eq),(.5,-1));

// un exemple analogue au précédent :  seul un point a changé !
// le script est le même à part les coordonnées du point pE.

// import geometry_dev; // extension devenue l'extension geometry officielle
import geometry;        // le 12/05/09, dans la version 1.71 d'asymptote. :-))

size(7.5cm,0);

show(currentcoordsys,dotpen=invisible);

point pA=(3,0), pB=(0,2), pC=(-4,0), pD=(0,-2), pE=(3,1);
dot(pA^^pB^^pC^^pD^^pE);

conic c = conic(pA,pB,pC,pD,pE);
draw(c,.8bp+.8green);

// equation(explicit conic co)
// est une fonction qui retourne l'équation d'une conique.
// sous la forme d'un objet bqe (repère + tableau des coefficients)
bqe eq = equation(c);
string[] b={"$x^2+$","$xy+$","$y^2+$","$x+$","$y+$","=0"};
string equ="L'\'equation de la conique est :\par";
for(int k=0; k<6; ++k) equ += format("(%.3f)",eq.a[k])+b[k];
equ += "\par (coefficients \'eventuellement arrondis)";
label(minipage(equ,width=250),(0,4));

// string conictype(bqe bqe)
// est une fonction qui retourne le type d'une conique.

label("La conique est de type : "+conictype(eq),(.5,-1));

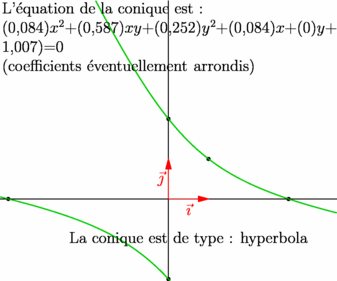
// un exemple analogue au précédent :  seul un point a changé !
// le script est le même à part les coordonnées du point pE.

// import geometry_dev; // extension devenue l'extension geometry officielle
import geometry;        // le 12/05/09, dans la version 1.71 d'asymptote. :-))

size(7.5cm,0);

show(currentcoordsys,dotpen=invisible);

point pA=(3,0), pB=(0,2), pC=(-4,0), pD=(0,-2), pE=(1,1);
dot(pA^^pB^^pC^^pD^^pE);

conic c = conic(pA,pB,pC,pD,pE);
draw(c,.8bp+.8green);

// equation(explicit conic co)
// est une fonction qui retourne l'équation d'une conique.
// sous la forme d'un objet bqe (repère + tableau des coefficients)
bqe eq = equation(c);
string[] b={"$x^2+$","$xy+$","$y^2+$","$x+$","$y+$","=0"};
string equ="L'\'equation de la conique est :\par";
for(int k=0; k<6; ++k) equ += format("(%.3f)",eq.a[k])+b[k];
equ += "\par (coefficients \'eventuellement arrondis)";
label(minipage(equ,width=250),(0,4));

// string conictype(bqe bqe)
// est une fonction qui retourne le type d'une conique.

label("La conique est de type : "+conictype(eq),(.5,-1));

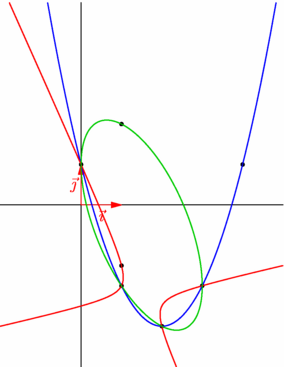
// un exemple analogue au précédent :  seul les points ont changé !
// le script est le même à part les coordonnées des 5 points.

// import geometry_dev; // extension devenue l'extension geometry officielle
import geometry;        // le 12/05/09, dans la version 1.71 d'asymptote. :-))

size(7.5cm,0);

show(currentcoordsys,dotpen=invisible);

transform t=shift((2,3))*rotate(135);
point pA=t*(-1,1), pB=t*(-.5,.25), pC=t*(0,0), pD=t*(1,1), pE=t*(2,4);
dot(pA^^pB^^pC^^pD^^pE);

conic c = conic(pA,pB,pC,pD,pE);
draw(c,.8bp+.8green);

// equation(explicit conic co)
// est une fonction qui retourne l'équation d'une conique.
// sous la forme d'un objet bqe (repère + tableau des coefficients)
bqe eq = equation(c);
string[] b={"$x^2+$","$xy+$","$y^2+$","$x+$","$y+$","=0"};
string equ="L'\'equation de la conique est :\par";
for(int k=0; k<6; ++k) equ += format("(%.3f)",eq.a[k])+b[k];
equ += "\par (coefficients \'eventuellement arrondis)";
label(minipage(equ,width=250),(0,4));

// string conictype(bqe bqe)
// est une fonction qui retourne le type d'une conique.

label("La conique est de type : "+conictype(eq),(.5,-1));

/* Une autre routine pour définir une conique est
       conic conic(point M1, point M2, point M3, point M4, point M5)
   qui retourne la conique non dégénérée passant par les 5 points.
*/
import geometry;
size(7.5cm,0);

show(currentcoordsys,dotpen=invisible);

point pA=(0,1), pB=(1,-2), pC=(2,-3), pD=(3,-2), pE=(4,1),
      pF=(1,-1.5), pG=(1,2);
dot(pA^^pB^^pC^^pD^^pE^^pF^^pG);

conic c1=conic(pA,pB,pC,pD,pE);
draw(c1,.8bp+blue);

conic c2=conic(pA,pB,pC,pD,pF);
draw(c2,.8bp+red);

conic c3=conic(pA,pB,pC,pD,pG);
draw(c3,.8bp+.8green);

draw(box((-2,-4), (5,5)), invisible);

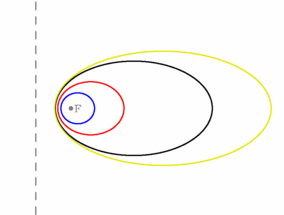
/* Ellipses obtenues avec la fonction conic
   qui renvoie un objet de type **conic**
   Remarque importante :
   Mais à partir de ce type **conic** ont été définis des
   types spécifiques : **circle**, **ellipse**, **parabola**,
   **hyperbola**. Donc pour tracer des ellipses, on utilisera
   plutôt la fonction ellipse qui renvoie un objet de type 
   **ellipse**. Cf. exemples suivants.
*/
// import geometry_dev; // extension devenue l'extension geometry officielle
import geometry;        // le 12/05/09, dans la version 1.71 d'asymptote. :-))

size(7.5cm,0);
point foyer=(0,0); dot("F", foyer, E, fontsize(8)+gray);

line directrice=line(1,0,1); // 1x+0y+1=0 ssi x=-1
draw(directrice,dashed+.7bp+gray);

// Lorsque 0 < e < 1, on obtient des ellipses.

conic ell2=conic(foyer,directrice,.4); // bleue
draw(ell2,.8bp+blue);

conic ell3=conic(foyer,directrice,.6); // rouge
draw(ell3,.8bp+red);

conic ell4=conic(foyer,directrice,.8); // noir
draw(ell4,.8bp+black);

conic ell5=conic(foyer,directrice,.85); // jaune
draw(ell5,.8bp+.9yellow);

draw(box((-2,-3), (6,3)), invisible);

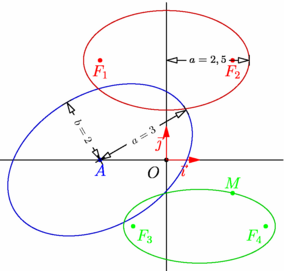
/* Ellipses obtenues avec la fonction ellipse
   qui renvoie un objet de type **ellipse**.
   Trois syntaxes possibles :
   - ellipse(point C, real a, real b, real angle=0)
     retourne l'ellipse de centre C dont le demi grand axe 
     a pour longueur a dans la direction donnée par dir(angle) 
     et dont le demi petit axe a pour longueur b.
   - ellipse(point F1, point F2, real a)
     retourne l'ellipse de foyers F1 et F2 dont le demi grand axe 
     a pour longueur a.
   - ellipse(point F1, point F2, point M)
     retourne l'ellipse de foyers F1 et F2 et passant par M.
*/
// import geometry_dev; // extension devenue l'extension geometry officielle
import geometry;        // le 12/05/09, dans la version 1.71 d'asymptote. :-))

size(7.5cm,0);
show(currentcoordsys);
// On définit...
point pA=(-2,0),
      pF1=(-2,3), pF2=(2,3),
          pF3=(-1,-2), pF4=(3,-2), pM=(2,-1);
ellipse ell1=ellipse(pA, 3, 2, 30); //Syntaxe 1
ellipse ell2=ellipse(pF1, pF2, 2.5); //Syntaxe 2
ellipse ell3=ellipse(pF3, pF4, pM); //Syntaxe 3
// ... puis on affiche :
dot("$A$",pA,S,blue);
dot("$F_1$",pF1,S,red); dot("$F_2$",pF2,S,red);
dot("$F_3$",pF3,SE,green); dot("$F_4$",pF4,SW,green); 
dot("$M$",pM,N,green);
draw(ell1,.8blue);
draw(ell2,.8red);
draw(ell3,.8green);
distance("$a=3$",ell1.C,point(ell1,0),0,fontsize(8pt));
distance("$b=2$",ell1.C,point(ell1,Relative(0.25)),0,fontsize(8pt));
distance("$a=2,5$",ell2.C,point(ell2,0),0,fontsize(8pt));

addMargins(.2cm,.2cm);

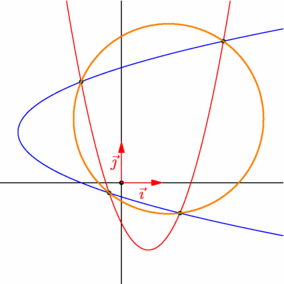
import geometry;
size(7.5cm,0);
show("",currentcoordsys);

real a=1.5,
     b=-2,
     c=-1, // coefficients de l'équation 1 : y=ax^2+bx+c
     d=1,
     e=-2.5,
     f=-1;   // coefficients de l'équation 2 : x=dy^2+ey+f

// Le type bqe, pour Bivariate Quadratic Equation, permet d'instancier un objet 
// représentant une équation de conique dans un repère donné.

// La fonction bqe(coordsys R=currentcoordsys,real a,real b,real c,real d,real e,real f)
// retourne un objet de type bqe représentant l'équation ax^2+bxy+cy^2+dx+ey+f=0 
// relativement au repère R.

bqe equation1=bqe(a,0,0,b,-1,c), // ax^2+bx-y+c=0
    equation2=bqe(0,0,d,-1,e,f); // dy^2-x+ey+f=0

conic parabole1=conic(equation1),
      parabole2=conic(equation2);
point[] ptsint=intersectionpoints(parabole1,parabole2);
circle  circ=circle(ptsint[0],ptsint[1],ptsint[2]);

draw(parabole1,red);
draw(parabole2,blue);
dot(ptsint,3bp+darkgreen);
draw(circ,1bp+orange);

draw(box((-3,-2.5),(4,4.5)),invisible);