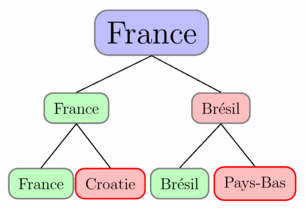
/*

ATTENTION ! Dans cette page, vous trouverez des arbres
            obtenus avec des méthodes différentes,
            et de niveaux de difficulté différents.
            On distinguera :
            - des exemples nécessitant l'extension drawtree ;
            - des exemples ne nécessitant aucun extension ;
            - des exemples nécessitant l'extension gm_probabilytree.

*/
import drawtree;

treeLevelStep = 1cm;
treeNodeStep = 0cm;

TreeNode RACINE = makeNode( "France" );
TreeNode DF1 = makeNode( RACINE, "France" );
TreeNode DF2 = makeNode( RACINE, "Br\'esil" );

TreeNode QF1 = makeNode( DF1, "France" );
TreeNode QF2 = makeNode( DF1, "Croatie" );
TreeNode QF3 = makeNode( DF2, "Br\'esil" );
TreeNode QF4 = makeNode( DF2, "Pays-Bas" );

draw(RACINE,(0,0));

shipout(bbox(5mm,white));

import drawtree;

treeLevelStep = 2cm;
treeNodeStep = 0cm;
treeMinNodeWidth = 1.8cm;
//-- Ajout d'un type de boite perso ---
TreeNode NodeGM( TreeNode parent = null, Label label, pen coul1=1bp+gray, pen coul2=paleblue )
{
  frame f;
  roundbox( f, label, xmargin=2mm, filltype=FillDraw(fillpen=coul2,drawpen=coul1) );
  return makeNode( parent, f );
}
//-------------------------------------

TreeNode RACINE = NodeGM( scale(2)*"France" ),
         DF1 = NodeGM( RACINE, "France", coul2=palegreen ),
         DF2 = NodeGM( RACINE, "Br\'esil", coul2=palered ),
         QF1 = NodeGM( DF1, "France", coul2=palegreen ),
         QF2 = NodeGM( DF1, "Croatie", coul1=1bp+red, coul2=palered ),
         QF3 = NodeGM( DF2, "Br\'esil", coul2=palegreen ),
         QF4 = NodeGM( DF2, "Pays-Bas", coul1=1bp+red, coul2=palered );

draw(RACINE,(0,0));

shipout(bbox(2mm,white));

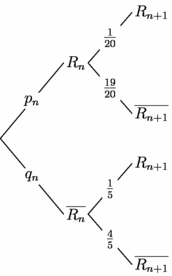
unitsize(1cm);

pen p=invisible;
real marge=0.2, EspH=2, EspV=2;

object objet_1=draw("$R_n$",box,(EspH,EspV),marge,p),
       objet_2=draw("$\overline{R_n}$",box,(EspH,-EspV),marge,p),
       objet_11=draw("$R_{n+1}$",box,(2*EspH,EspV*5/3),marge,p),
       objet_12=draw("$\overline{R_{n+1}}$",box,(2*EspH,EspV*1/3),marge,p),
       objet_21=draw("$R_{n+1}$",box,(2*EspH,-EspV*1/3),marge,p),
       objet_22=draw("$\overline{R_{n+1}}$",box,(2*EspH,-EspV*5/3),marge,p);

add(new void(picture pic, transform t) {
    draw(pic,Label("$p_n$",UnFill(1)),(0,0)--point(objet_1,W,t),Center);
    draw(pic,Label("$q_n$",UnFill(1)),(0,0)--point(objet_2,W,t),Center);
    draw(pic,Label("$\frac{1}{20}$",UnFill(1)),point(objet_1,E,t)--point(objet_11,W,t),Center);
    draw(pic,Label("$\frac{19}{20}$",UnFill(1)),point(objet_1,E,t)--point(objet_12,W,t),Center);
    draw(pic,Label("$\frac{1}{5}$",UnFill(1)),point(objet_2,E,t)--point(objet_21,W,t),Center);
    draw(pic,Label("$\frac{4}{5}$",UnFill(1)),point(objet_2,E,t)--point(objet_22,W,t),Center);
});

// Voir le même arbre dans les exemples suivants
// obtenu avec l'extension(ette) gm_probabilytree :
// la syntaxe s'en trouve simplifiée.

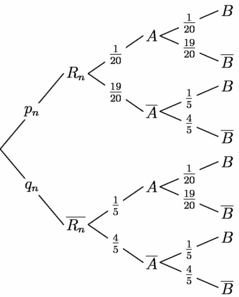
unitsize(1cm);

pen p=invisible;
real marge=0.2, EspH=2, EspV=2;

object objet_1=draw("$R_n$",box,(EspH,EspV),marge,p),
       objet_2=draw("$\overline{R_n}$",box,(EspH,-EspV),marge,p),
       objet_11=draw("$A$",box,(2*EspH,EspV*3/2),marge,p),
       objet_12=draw("$\overline{A}$",box,(2*EspH,EspV*1/2),marge,p),
       objet_21=draw("$A$",box,(2*EspH,-EspV*1/2),marge,p),
       objet_22=draw("$\overline{A}$",box,(2*EspH,-EspV*3/2),marge,p),
       objet_111=draw("$B$",box,(3*EspH,EspV*11/6),marge,p),
       objet_112=draw("$\overline{B}$",box,(3*EspH,EspV*7/6),marge,p),
       objet_121=draw("$B$",box,(3*EspH,EspV*5/6),marge,p),
       objet_122=draw("$\overline{B}$",box,(3*EspH,EspV*1/6),marge,p),
       objet_211=draw("$B$",box,(3*EspH,-EspV*1/6),marge,p),
       objet_212=draw("$\overline{B}$",box,(3*EspH,-EspV*5/6),marge,p),
       objet_221=draw("$B$",box,(3*EspH,-EspV*7/6),marge,p),
       objet_222=draw("$\overline{B}$",box,(3*EspH,-EspV*11/6),marge,p);

add(new void(picture pic, transform t) {
    draw(pic,Label("$p_n$",UnFill(1)),(0,0)--point(objet_1,W,t),Center);
    draw(pic,Label("$q_n$",UnFill(1)),(0,0)--point(objet_2,W,t),Center);
    draw(pic,Label("$\frac{1}{20}$",UnFill(1)),point(objet_1,E,t)--point(objet_11,W,t),Center);
    draw(pic,Label("$\frac{19}{20}$",UnFill(1)),point(objet_1,E,t)--point(objet_12,W,t),Center);
    draw(pic,Label("$\frac{1}{5}$",UnFill(1)),point(objet_2,E,t)--point(objet_21,W,t),Center);
    draw(pic,Label("$\frac{4}{5}$",UnFill(1)),point(objet_2,E,t)--point(objet_22,W,t),Center);
    draw(pic,Label("$\frac{1}{20}$",UnFill(1)),point(objet_11,E,t)--point(objet_111,W,t),Center);
    draw(pic,Label("$\frac{19}{20}$",UnFill(1)),point(objet_11,E,t)--point(objet_112,W,t),Center);
    draw(pic,Label("$\frac{1}{5}$",UnFill(1)),point(objet_12,E,t)--point(objet_121,W,t),Center);
    draw(pic,Label("$\frac{4}{5}$",UnFill(1)),point(objet_12,E,t)--point(objet_122,W,t),Center);
    draw(pic,Label("$\frac{1}{20}$",UnFill(1)),point(objet_21,E,t)--point(objet_211,W,t),Center);
    draw(pic,Label("$\frac{19}{20}$",UnFill(1)),point(objet_21,E,t)--point(objet_212,W,t),Center);
    draw(pic,Label("$\frac{1}{5}$",UnFill(1)),point(objet_22,E,t)--point(objet_221,W,t),Center);
    draw(pic,Label("$\frac{4}{5}$",UnFill(1)),point(objet_22,E,t)--point(objet_222,W,t),Center);
});

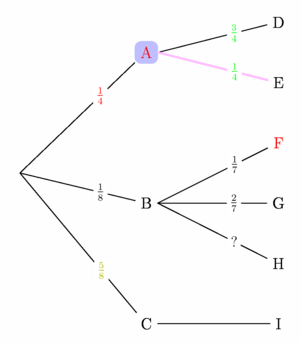
// gm_probabilitytree.asy
// Extension destinée à dessiner un arbre de probabilités
// C'est une première version, non documentée, en phase de test,
// téléchargeable ici : gm_probabilitytree.asy

import gm_probabilitytree;

// Cette extension perso définit (entre autres choses à venir) :
// 1. la structure 'Noeud'
// 2. la fonction addN pour créer les noeuds de l'arbre pondéré
//    suivant la syntaxe :
//    Noeud addN( Noeud parent = null, 
//                Label evenement = "", 
//                pen[] evpen={currentpen,invisible},
//                Label probabilite = "", 
//                pen   prpen=currentpen)
// 3. la commande TracerArbre qui fait ce que son nom dit.

// Paramètres par défaut de l'arbre :
/* DistVertEntreNoeuds = .5cm;
   DistHoriEntreNiveaux = 2cm;
   HauteurNoeudMinimale = 1cm;
   StyleEvenParDefaut = 1bp+black;
   StyleBackGrParDefaut = invisible;
   StyleProbParDefaut = black;
*/

// Définition de styles particuliers pour les événements
// suivant la syntaxe :
//      pen[] p={couleur du texte}
// ou   pen[] p={couleur du texte,couleur arrière plan}
pen[] p1={red,paleblue};
pen[] p2={red};

DistVertEntreNoeuds = 1cm;
DistHoriEntreNiveaux = 3.5cm;
HauteurNoeudMinimale = .5cm;
StyleEvenParDefaut = 1bp+black;
StyleBackGrParDefaut = invisible;
StyleProbParDefaut = black;
StyleBrParDefaut = black;

// Définition de la structure de l'arbre
Noeud   RAC = addN( ),
        Na = addN( RAC, "A", p1, "$\frac{1}{4}$", red ),
        Nb = addN( RAC, "B", "$\frac{1}{8}$" ),
        Nc = addN( RAC, "C", "$\frac{5}{8}$", .7yellow ),
        Nd = addN( Na, "D", "$\frac{3}{4}$", green ),
        Ne = addN( Na, "E", "$\frac{1}{4}$", green, 1.5bp+pink ),
        Nf = addN( Nb, "F", p2, "$\frac{1}{7}$" ),
        Ng = addN( Nb, "G", "$\frac{2}{7}$" ),
        Nh = addN( Nb, "H", "?"),
        Ni = addN( Nc, "I" );

// Tracé de l'arbre
TracerArbre(racine=RAC,pos=(0,0));

shipout(bbox(2mm,white));

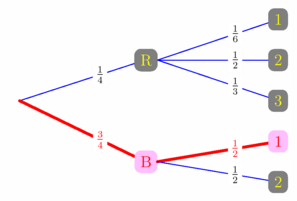
// gm_probabilitytree.asy
// Extension destinée à dessiner un arbre de probabilités
// C'est une première version, non documentée, en phase de test,
// téléchargeable ici : gm_probabilitytree.asy

import gm_probabilitytree;

pen[] p1={yellow,gray};
pen[] p2={red, pink};

DistVertEntreNoeuds = .5cm;
DistHoriEntreNiveaux = 3.5cm;
HauteurNoeudMinimale = .5cm;
StyleEvenParDefaut = 1bp+black;
StyleBackGrParDefaut = invisible;
StyleProbParDefaut = black;
StyleBrParDefaut = blue;

// Définition de la structure de l'arbre
Noeud   RAC = addN( ),
        NR  = addN( RAC, "R", p1, "$\frac{1}{4}$" ),
        NB  = addN( RAC, "B", p2, "$\frac{3}{4}$", red, 2bp+red ),
        Nra = addN( NR, "1", p1, "$\frac{1}{6}$" ),
        Nrb = addN( NR, "2", p1, "$\frac{1}{2}$" ),
        Nrc = addN( NR, "3", p1, "$\frac{1}{3}$" ),
        Nba = addN( NB, "1", p2, "$\frac{1}{2}$", red, 2bp+red ),
        Nbb = addN( NB, "2", p1, "$\frac{1}{2}$" );

// Tracé de l'arbre
TracerArbre(racine=RAC,pos=(0,0));

shipout(bbox(2mm,white));

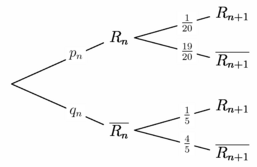
// gm_probabilitytree.asy
// Extension destinée à dessiner un arbre de probabilités
// C'est une première version, non documentée, en phase de test,
// téléchargeable ici : gm_probabilitytree.asy

import gm_probabilitytree;

DistHoriEntreNiveaux = 3cm;

Noeud RAC = addN( ),
      n1a = addN( RAC, "$R_n$",            "$p_n$" ),
      n1b = addN( RAC, "$\overline{R_n}$", "$q_n$" );

// Quatre noeuds qui ne necéssitent pas d'être nommmés.      
addN( n1a, "$R_{n+1}$",            "$\frac{1}{20}$" );
addN( n1a, "$\overline{R_{n+1}}$", "$\frac{19}{20}$" );
addN( n1b, "$R_{n+1}$",            "$\frac{1}{5}$" );
addN( n1b, "$\overline{R_{n+1}}$", "$\frac{4}{5}$" );

TracerArbre(RAC);

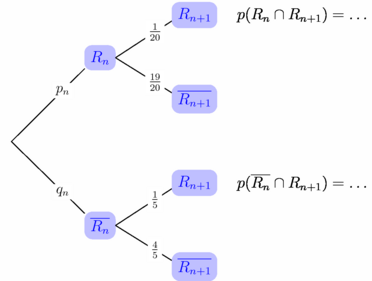
// gm_probabilitytree.asy
// Extension destinée à dessiner un arbre de probabilités
// C'est une première version, non documentée, en phase de test,
// téléchargeable ici : gm_probabilitytree.asy

import gm_probabilitytree;

pen[] p1={blue,paleblue};
DistVertEntreNoeuds = 1.5cm;
DistHoriEntreNiveaux = 2.5cm;

Noeud RAC = addN( ),
      n1a = addN( RAC, "$R_n$",            p1, "$p_n$" ),
      n1b = addN( RAC, "$\overline{R_n}$", p1, "$q_n$" ),
      n2a = addN( n1a, "$R_{n+1}$",        p1, "$\frac{1}{20}$" ),
      n2c = addN( n1b, "$R_{n+1}$",        p1, "$\frac{1}{5}$" );      

// Deux noeuds qui ne necéssitent pas d'être nommmés.      
addN( n1a, "$\overline{R_{n+1}}$", p1, "$\frac{19}{20}$" );
addN( n1b, "$\overline{R_{n+1}}$", p1, "$\frac{4}{5}$" );

TracerArbre(RAC);

transform t=shift(1cm,0);
label("$p(R_n\cap R_{n+1})=\dots$",t*n2a,align=E);
label("$p(\overline{R_n}\cap R_{n+1})=\dots$",t*n2c,align=E);

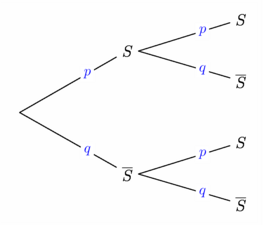
// gm_probabilitytree.asy
// Extension destinée à dessiner un arbre de probabilités
// C'est une première version, non documentée, en phase de test,
// téléchargeable ici : gm_probabilitytree.asy

import gm_probabilitytree;

DistVertEntreNoeuds = 1cm;
DistHoriEntreNiveaux = 3cm;
HauteurNoeudMinimale = .5cm;
StyleEvenParDefaut = 1bp+black;
StyleBackGrParDefaut = invisible;
StyleProbParDefaut = blue;

// Tracé de l'arbre relatif à un schéma de Bernouilli
// par défaut : 2 répétitions, succès noté S.
Bernouilli();
// Syntaxe :
// void Bernouilli(Label Succes="$S$", Label probS="$p$",
//                 Label Echec="$\overline{S}$", Label probE="$q$",
//                 int repet=2, pair pos=(0,0))

shipout(bbox(2mm,white));

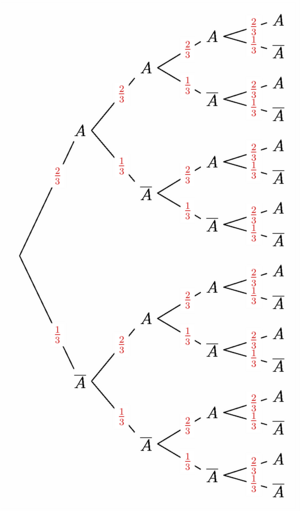
// gm_probabilitytree.asy
// Extension destinée à dessiner un arbre de probabilités
// C'est une première version, non documentée, en phase de test,
// téléchargeable ici : gm_probabilitytree.asy

import gm_probabilitytree;

DistVertEntreNoeuds = .2cm; // entre noeuds "terminaux"
DistHoriEntreNiveaux = 1.75cm;
HauteurNoeudMinimale = .2cm;
StyleEvenParDefaut = 1bp+black;
StyleBackGrParDefaut = invisible;
StyleProbParDefaut = .8red;

// Tracé de l'arbre relatif à un schéma de Bernouilli
Bernouilli(Succes="$A$", probS="$\frac{2}{3}$",
           Echec="$\overline{A}$", probE="$\frac{1}{3}$",
           repet=4, pos=(0,0));
// Syntaxe :
// void Bernouilli(Label Succes="$S$", Label probS="$p$",
//                 Label Echec="$\overline{S}$", Label probE="$q$",
//                 int repet=2, pair pos=(0,0))

shipout(bbox(2mm,white));

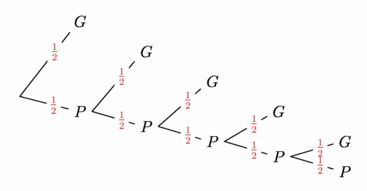
// gm_probabilitytree.asy
// Extension destinée à dessiner un arbre de probabilités
// C'est une première version, non documentée, en phase de test,
// téléchargeable ici : gm_probabilitytree.asy

import gm_probabilitytree;

DistVertEntreNoeuds = .2cm; // entre noeuds "terminaux"
DistHoriEntreNiveaux = 1.75cm;
HauteurNoeudMinimale = .2cm;
StyleEvenParDefaut = 1bp+black;
StyleBackGrParDefaut = invisible;
StyleProbParDefaut = .8red;

// Je joue tant que je ne gagne pas :
GagnerAToutPrix();
// Syntaxe :
// void GagnerAToutPrix( Label Succes="$G$", Label probS="$\frac{1}{2}$",
//                       Label Echec="$P$", Label probE="$\frac{1}{2}$",
//                       int repet=4, pair pos=(0,0) )
shipout(bbox(2mm,white));