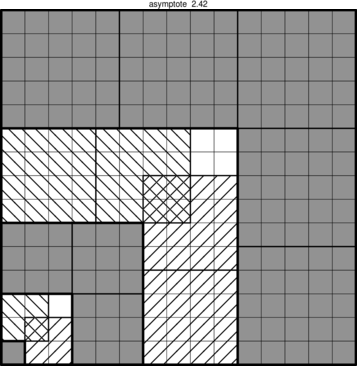
*** Pour masquer/découvrir le code Asymptote qui a permis de créer la figure, il faut cliquer dessus. ;-) ***
- CODE ASYMPTOTE de la figure ci-dessus : Tout sélectionner
- size(200,0);
- import patterns;
- add("hatch",hatch(2mm));
- add("hatchback",hatch(2mm,NW));
- add("crosshatch",crosshatch(2mm));
- path p=unitsquare;
- for(int i=0;i<15;++i)
- {
- for (int j=0;j<15;++j)
- {
- draw(shift(i,j)*p);
- }
- }
- filldraw(p,gray);
- path p1=scale(2)*p;
- filldraw(shift(0,1)*p1,pattern("hatch"));
- filldraw(shift(1,0)*p1,pattern("hatch"));
- filldraw(shift(1,1)*p,pattern("crosshatch"));
- path p2=scale(3)*p;
- filldraw(shift(3,0)*p2,gray);
- filldraw(shift(3,3)*p2,gray);
- filldraw(shift(0,3)*p2,gray);
- path p3=scale(4)*p;
- filldraw(shift(6,0)*p3,pattern("hatch"));
- filldraw(shift(4,6)*p3,pattern("hatch"));
- filldraw(shift(0,6)*p3,pattern("hatch"));
- filldraw(shift(6,4)*p3,pattern("hatch"));
- filldraw(shift(6,6)*p1,pattern("crosshatch"));
- filldraw(shift(8,8)*p1,white);
- path p4=scale(5)*p;
- filldraw(shift(10,0)*p4,gray);
- filldraw(shift(10,5)*p4,gray);
- filldraw(shift(0,10)*p4,gray);
- filldraw(shift(10,10)*p4,gray);
- filldraw(shift(5,10)*p4,gray);
- for(int i=0;i<15;++i)
- {
- for (int j=0;j<15;++j)
- {
- draw(shift(i,j)*p);
- }
- }
- filldraw(shift(8,8)*p1,white);
- draw(p,black+1.5bp);
- draw(scale(3)*p,black+1.5bp);
- draw(scale(6)*p,black+1.5bp);
- draw(scale(10)*p,black+1.5bp);
- draw(scale(15)*p,black+1.5bp);
Permet en clignant des yeux de trouver la formule
 .
.