Comment tailler un short ?
Règles du forum
Pour toute demande d'aide pour la conception (ou la confirmation d'un code) d'une figure Asymptote, c'est ici.
J'invite ceux qui ont régulièrement des questions à poser à aller dans leur panneau de l'utilisateur pour indiquer dans la signature de leurs messages :
On va gagner du temps dans les réponses !
Pour toute demande d'aide pour la conception (ou la confirmation d'un code) d'une figure Asymptote, c'est ici.
J'invite ceux qui ont régulièrement des questions à poser à aller dans leur panneau de l'utilisateur pour indiquer dans la signature de leurs messages :
- Nom du système d'exploitation (W7 ou Ubuntu 12.04 ou ...)
- Version d'Asymptote et éditeur utilisé pour les figures Asymptote
- Distribution LaTeX et éditeur utilisé pour les tex.
On va gagner du temps dans les réponses !
Comment tailler un short ?
Sous ce titre amusant se cache une question pour aider un ami enseignant à la fac.
Un short (ou plutôt) un pantalon est une surface ayant trois manchon, un pour le tronc et deux pour les jambes.
Je cherche à lui dessiner ça avec asymptote, d'abord un short.
Puis je pense à un petit programme python qui crachera le code pour un pantalon avec 6 paramètres, les trois (centres des sorties avec un vecteur normal dont la norme donnera le rayon de sortie) ...
À terme, c'est pour associer de nombreux pantalons en les connectant, et faire des surfaces de plus en plus complexes ...
Il me faut donc une technique qui soit la plus légère possible pour la compilation et la manipulation PRC.
J'ai pensé aux surfaces de Bezier, est-ce une bonne idée ?
Je crois pouvoir faire un pantalon avec 4*3=12 triangles, ou alors avec moins de quadrilatère.
J'ai bien compris comment ça fonctionne avec les quadrilatère, mais je pèche sur les triangles.
J'ai juste compris que la première colonne était composée d'un point de contrôle unique, mais j'ai du mal avec les points de contrôle au centre.
------
1) Surfaces de Bezier, bonne idée ? Ou alors tout faire en analytique ?
2) Vaut-il mieux choisir des triangles ou des quadrilatères ?
2bis) une petite explication sur les triangles serait super.
3) J'ai vu la fonction "patch" trainer, mais j'ai pas compris son utilité.
Merci beaucoup pour toute aide.
Un short (ou plutôt) un pantalon est une surface ayant trois manchon, un pour le tronc et deux pour les jambes.
Je cherche à lui dessiner ça avec asymptote, d'abord un short.
Puis je pense à un petit programme python qui crachera le code pour un pantalon avec 6 paramètres, les trois (centres des sorties avec un vecteur normal dont la norme donnera le rayon de sortie) ...
À terme, c'est pour associer de nombreux pantalons en les connectant, et faire des surfaces de plus en plus complexes ...
Il me faut donc une technique qui soit la plus légère possible pour la compilation et la manipulation PRC.
J'ai pensé aux surfaces de Bezier, est-ce une bonne idée ?
Je crois pouvoir faire un pantalon avec 4*3=12 triangles, ou alors avec moins de quadrilatère.
J'ai bien compris comment ça fonctionne avec les quadrilatère, mais je pèche sur les triangles.
J'ai juste compris que la première colonne était composée d'un point de contrôle unique, mais j'ai du mal avec les points de contrôle au centre.
------
1) Surfaces de Bezier, bonne idée ? Ou alors tout faire en analytique ?
2) Vaut-il mieux choisir des triangles ou des quadrilatères ?
2bis) une petite explication sur les triangles serait super.
3) J'ai vu la fonction "patch" trainer, mais j'ai pas compris son utilité.
Merci beaucoup pour toute aide.
Re: Comment tailler un short ?
Pas facile de créer une telle surface. Tu aurais pu préférer une amie
de fac qui demande une jupe tout de même.
As-tu déjà un lien montrant un tel short ?
Est-ce lié à un objet mathématique ?
Pour les triangles vs les quadrilatères la seule différence
pour asymptote sera que pour le triangle on donne des points
en plus qui coïncident avec d'autres points (grosso modo si
on devait juste donner les trois sommets on donne quatre points
et le dernier étant un des sommets, pour la surface de Bézier
il faut réfléchir alors un peu histoire de ne pas mettre le bazar).
16 points de contrôle pour le quadrilatère et pour le triangle
je ne sais plus.
Il y a (avait) une animation de Philippe pour voir un peu.
Sinon en dehors d'Asymptote, ce genre de chose est documentée.
Avec une forme analytique ce serait tout de même plus
facile. Sinon à l'aide d'une couturière qui a un gabarit, un dispositif
laser qui te triangularise ton short ce serait un premier pas.
Pour les 16 points de contrôles, 4 sont les extrémités, 4 paquets
de deux seront les dérivées le long du bord, et les 4 autres doivent
pouvoir correspondre à une dérivée seconde ou un truc du genre.
Pour une surface composée de carreaux de Bézier, les points de contrôle
autre que les extrémités permettent d'avoir le côté lisse, la régularité
 ou
ou 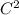 de ta surface entière.
de ta surface entière.
J'oubliais : un logiciel de CAO 3D pourra aider aussi.
O.G.
de fac qui demande une jupe tout de même.
As-tu déjà un lien montrant un tel short ?
Est-ce lié à un objet mathématique ?
Pour les triangles vs les quadrilatères la seule différence
pour asymptote sera que pour le triangle on donne des points
en plus qui coïncident avec d'autres points (grosso modo si
on devait juste donner les trois sommets on donne quatre points
et le dernier étant un des sommets, pour la surface de Bézier
il faut réfléchir alors un peu histoire de ne pas mettre le bazar).
16 points de contrôle pour le quadrilatère et pour le triangle
je ne sais plus.
Il y a (avait) une animation de Philippe pour voir un peu.
Sinon en dehors d'Asymptote, ce genre de chose est documentée.
Avec une forme analytique ce serait tout de même plus
facile. Sinon à l'aide d'une couturière qui a un gabarit, un dispositif
laser qui te triangularise ton short ce serait un premier pas.
Pour les 16 points de contrôles, 4 sont les extrémités, 4 paquets
de deux seront les dérivées le long du bord, et les 4 autres doivent
pouvoir correspondre à une dérivée seconde ou un truc du genre.
Pour une surface composée de carreaux de Bézier, les points de contrôle
autre que les extrémités permettent d'avoir le côté lisse, la régularité
 ou
ou 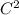 de ta surface entière.
de ta surface entière.J'oubliais : un logiciel de CAO 3D pourra aider aussi.
O.G.
Re: Comment tailler un short ?
Code : Tout sélectionner
import solids;
currentprojection=orthographic(
camera=(6.313276862811,6.61829365428347,-2.68091042395435),
up=(0.0101527637607303,0.000472445029074958,0.0250750263559901),
target=(2.87096735274162e-16,1.57209315010398e-15,1.98495733738646e-15),
zoom=0.613913253540759);
size(7.5cm);
real a=1, b=2;
transform3 sOYZ=reflect(O,Y,Z),tOY=shift(a*Y), tOX=shift(a*X), sOXZ=reflect(O,X,Z), rOZ=rotate(180,Z);
path3 p=(a,0,0)--(a,0,-2b);
revolution s=revolution(p,Z,0,90);
triple[][] P3={
{(a,0,-b),(a,a/2,-b),(a,a/2,-b),(a,a,-b)},
{(a,0,-4b/3),(2a/3,a/3,-4b/3),(2a/3,2a/3,-4b/3),(a,a,-4b/3)},
{(2a/3,0,-4b/3),(a/3,a/3,-4b/3),(2a/3,2a/3,-4b/3),(a,a,-4b/3)},
{(0,0,-3b/2),(a/3,0,-3b/2),(a,2a/3,-3b/2),(a,a,-3b/2)}
};
triple[][] P4={
{(0,0,-3b/2),(a/3,0,-3b/2),(a,2a/3,-3b/2),(a,a,-3b/2)},
{(0,0,-5b/3),(a/3,a/3,-5b/3),(a,2a/3,-5b/3),(a,a,-5b/3)},
{(0,a/5,-5b/3),(a/3,a/3,-5b/3),(a,2a/3,-5b/3),(a,a,-5b/3)},
{(0,a/5,-2b),(a/3,a/5,-2b),(a,2a/3,-2b),(a,a,-2b)}
};
surface s1=tOY*surface(s),
s2=tOX*surface(O--(0,a,0)--(0,a,-b)--(0,0,-b)--cycle),
s3=surface(patch(P3)),
s4=surface(patch(P4));
draw(s1,lightblue);
draw(sOYZ*s1,lightblue);
draw(sOXZ*s1,lightblue);
draw(rOZ*s1,lightblue);
draw(s2,lightblue);
draw(sOYZ*s2,lightblue);
draw(sOXZ*s2,lightblue);
draw(rOZ*s2,lightblue);
draw(s3,lightblue);
draw(sOYZ*s3,lightblue);
draw(sOXZ*s3,lightblue);
draw(rOZ*s3,lightblue);
draw(s4,lightblue);
draw(sOYZ*s4,lightblue);
draw(sOXZ*s4,lightblue);
draw(rOZ*s4,lightblue);
limits(O,1.5*(X+Y+Z));
xaxis3(scale(1.5)*Label("$x$",1),1bp+green,Arrow3);
yaxis3(scale(1.5)*Label("$y$",1),1bp+green,Arrow3);
zaxis3(scale(1.5)*Label("$z$",1),1bp+green,Arrow3);
Je sais que c'est nul (baclé en 20 mn)... mais c'était histoire qu'il y ait au moins une proposition.
Index des fonctions - Exemple de lien donnant le résultat d'une recherche sur les mots 'arc' et 'triple' : http://asy.marris.fr/indexasy/?filtre=arc triple
Mes configurations (le 24/02/21) :
PC n°1 :Windows 10 - Asymptote(2.82)+MikTeX2.9 - Editeurs : Notepad++, TeXworks, Visual Studio Code.
PC n°2 : Ubuntu 20.04LTS - Asymptote(2.67-?? git) + TexLive2020
Mon serveur : Debian Stretch- Asymptote(2.68-16 git) + TexLive2018
Merci de préciser la votre !
Mes configurations (le 24/02/21) :
PC n°1 :Windows 10 - Asymptote(2.82)+MikTeX2.9 - Editeurs : Notepad++, TeXworks, Visual Studio Code.
PC n°2 : Ubuntu 20.04LTS - Asymptote(2.67-?? git) + TexLive2020
Mon serveur : Debian Stretch- Asymptote(2.68-16 git) + TexLive2018
Merci de préciser la votre !
Re: Comment tailler un short ?
Merci pour cet exemple et les explications.
C'est l'objet mathématique et non le vêtement qui m'intéresse.
Pour mes questions, je rappelle que j'avais déjà compris les quadrilatères et leur 16 points de contrôle...
1) Mais quid exactement des triangles ? Je ne comprends exactement pas le "centre" de la matrice.
Je sais qu'on peut rendre un ensemble de triangle C2, mais comment ?
Où avez vous trouvé une doc ? Merci.
2) Et ""patch"", c'est quoi, est-ce nécessaire ? Ça change quoi ?
3) Et question rapidité, est-ce mieux que de l'analytique ? (Je compte faire des figures avec une dizaine de short connectés)
4) BONUS -- J'ai vu que l'on pouvait tracer des courbes sur ces quadrilatères, avec vequals ou uequals, qui donnent les parallèles.
Mais peut-on y aller en diagonale. Ça m'intéresse beaucoup.
C'est l'objet mathématique et non le vêtement qui m'intéresse.
Pour mes questions, je rappelle que j'avais déjà compris les quadrilatères et leur 16 points de contrôle...
1) Mais quid exactement des triangles ? Je ne comprends exactement pas le "centre" de la matrice.
Je sais qu'on peut rendre un ensemble de triangle C2, mais comment ?
Où avez vous trouvé une doc ? Merci.
2) Et ""patch"", c'est quoi, est-ce nécessaire ? Ça change quoi ?
3) Et question rapidité, est-ce mieux que de l'analytique ? (Je compte faire des figures avec une dizaine de short connectés)
4) BONUS -- J'ai vu que l'on pouvait tracer des courbes sur ces quadrilatères, avec vequals ou uequals, qui donnent les parallèles.
Mais peut-on y aller en diagonale. Ça m'intéresse beaucoup.
Re: Comment tailler un short ?
Bonsoir
Avec asymptote, une surface est composée de plusieurs carreaux
(ou patch). Le patch est la brique élémentaire. Par exemple
pour générer la surface z=f(x,y), sur un pavé en x,y on fait
des carreaux et on peut choisir ce nombre de carreaux.
Comme pour les courbes spline cubiques par morceaux, on peut
s'arranger via des conditions de raccords sur les bords à avoir
une surface lisse (et pas des facettes), (plus sûr que
(plus sûr que
la surface soit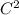 ). C'est ce genre de chose qui rend asymptote
). C'est ce genre de chose qui rend asymptote
assez attrayant.
Le patch est un carreau de Bézier, bicubique d'où les 16 points
de contrôle. Pour le triangle c'est juste un artifice : un quadrilatère
avec deux points confondus devient un triangle. Le triangle n'est donc
pas à proprement gérer par asymptote (il y a les autres points de contrôles).
En fouillant dans three_surface on voit par exemple comment est définie
la sphére
Ici patch prend comme argument un chemin de longueur 4 (deux points confondus)
et un tableau de vecteurs optionnel (le seul chemin ne suffit pas à déterminer
un unique carreau de Bézier bicubique). Pour la signification de ces vecteurs
je ne sais pas trop, mais c'est lié à des dérivées. Tout a lieu ligne 217
de three_surface.asy avec
Question lien, je n'en ai pas sous la main. Si ton ami est matheux
il a la possibilité d'accéder à des bibliothèques fournies.
Je réitère : quelle origine mathématique de cet objet ?
Comme un carreau est une bicubique, on doit pouvoir accéder à
 :
:
Question analytique, il faudrait déjà avoir une description
analytique du short, ce qui peut aussi aider à construire.
O.G.
Avec asymptote, une surface est composée de plusieurs carreaux
(ou patch). Le patch est la brique élémentaire. Par exemple
pour générer la surface z=f(x,y), sur un pavé en x,y on fait
des carreaux et on peut choisir ce nombre de carreaux.
Comme pour les courbes spline cubiques par morceaux, on peut
s'arranger via des conditions de raccords sur les bords à avoir
une surface lisse (et pas des facettes),
 (plus sûr que
(plus sûr quela surface soit
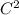 ). C'est ce genre de chose qui rend asymptote
). C'est ce genre de chose qui rend asymptoteassez attrayant.
Le patch est un carreau de Bézier, bicubique d'où les 16 points
de contrôle. Pour le triangle c'est juste un artifice : un quadrilatère
avec deux points confondus devient un triangle. Le triangle n'est donc
pas à proprement gérer par asymptote (il y a les autres points de contrôles).
En fouillant dans three_surface on voit par exemple comment est définie
la sphére
Code : Tout sélectionner
private real a=4/3*(sqrt(2)-1);
private transform3 t1=rotate(90,O,Z);
private transform3 t2=t1*t1;
private transform3 t3=t2*t1;
private transform3 i=xscale3(-1)*zscale3(-1);
restricted patch octant1=patch(X{Y}..{-X}Y{Z}..{-Y}Z..Z{X}..{-Z}cycle,
new triple[] {(1,a,a),(a,1,a),(a^2,a,1),
(a,a^2,1)});
restricted surface unithemisphere=surface(octant1,t1*octant1,t2*octant1,
t3*octant1);
restricted surface unitsphere=surface(octant1,t1*octant1,t2*octant1,t3*octant1,
i*octant1,i*t1*octant1,i*t2*octant1,
i*t3*octant1);
Ici patch prend comme argument un chemin de longueur 4 (deux points confondus)
et un tableau de vecteurs optionnel (le seul chemin ne suffit pas à déterminer
un unique carreau de Bézier bicubique). Pour la signification de ces vecteurs
je ne sais pas trop, mais c'est lié à des dérivées. Tout a lieu ligne 217
de three_surface.asy avec
Code : Tout sélectionner
// A constructor for a convex cyclic path3 of length <= 4 with optional
// arrays of 4 internal points, corner normals, and pens.
void operator init(path3 external, triple[] internal=new triple[],
triple[] normals=new triple[], pen[] colors=new pen[],
bool3 planar=default) {
Question lien, je n'en ai pas sous la main. Si ton ami est matheux
il a la possibilité d'accéder à des bibliothèques fournies.
Je réitère : quelle origine mathématique de cet objet ?
Comme un carreau est une bicubique, on doit pouvoir accéder à
 :
:Code : Tout sélectionner
guide3 g;
for (int i=0;i<11 ;++i ) {
g=g..octant1.point(i/10,i/10);
}
draw(g,red);
Question analytique, il faudrait déjà avoir une description
analytique du short, ce qui peut aussi aider à construire.
O.G.
Re: Comment tailler un short ?
Pas du tout le temps de m'occuper d'asymptote depuis un mois... et il devrait en être de même en août.
Donc je me contente de lire rapidement ce qu'il se dit...
... et de balancer une figure de temps en temps.
Voilà, en images, le "surface(octant1)" (du code cité par Olivier), à la base de la création d'une sphère :
Les points rouges correspondent à : (1,a,a),(a,1,a),(a^2,a,1),(a,a^2,1).
Donc je me contente de lire rapidement ce qu'il se dit...
... et de balancer une figure de temps en temps.
Voilà, en images, le "surface(octant1)" (du code cité par Olivier), à la base de la création d'une sphère :
Les points rouges correspondent à : (1,a,a),(a,1,a),(a^2,a,1),(a,a^2,1).
Index des fonctions - Exemple de lien donnant le résultat d'une recherche sur les mots 'arc' et 'triple' : http://asy.marris.fr/indexasy/?filtre=arc triple
Mes configurations (le 24/02/21) :
PC n°1 :Windows 10 - Asymptote(2.82)+MikTeX2.9 - Editeurs : Notepad++, TeXworks, Visual Studio Code.
PC n°2 : Ubuntu 20.04LTS - Asymptote(2.67-?? git) + TexLive2020
Mon serveur : Debian Stretch- Asymptote(2.68-16 git) + TexLive2018
Merci de préciser la votre !
Mes configurations (le 24/02/21) :
PC n°1 :Windows 10 - Asymptote(2.82)+MikTeX2.9 - Editeurs : Notepad++, TeXworks, Visual Studio Code.
PC n°2 : Ubuntu 20.04LTS - Asymptote(2.67-?? git) + TexLive2020
Mon serveur : Debian Stretch- Asymptote(2.68-16 git) + TexLive2018
Merci de préciser la votre !
Re: Comment tailler un short ?
Pour l'origine mathématique du "pantalon".
Il y a un théorème qui dit vaguement qu'une surface convexe, compacte, et avec des trous
peut être vue comme une associations de pantalon.
Il s'intéresse aux classes d'équivalences.
Un tore à deux trous, est dans la classe de deux pantalons raboutés par le tronc.
Les pattes de chaque pantalon se soudent face à face.
Ainsi peu importe la définition analytique à partir du moment où un bretzel a bien 3 trous ...
--------------
Il souhaite dessiner de nombreux pantalons, et je vais essayer de lui proposer un programme python (ou autre)
qui crache le bon code asymptote.
Il me faut une fonction pantalon à 6 paramètres.
3 points de sortie, et trois vecteurs "débit" associés.
Et oui, les manchons ne sont pas forcément parallèles.
Plus le débit est gros, plus le "disque" sera large. Le débit est normal à ce disque.
--------------
Je dit "disque" car, si j'ai bien compris, les surfaces de Bézier ne fournissent qu'une "très bonne" approximation du disque.
Et ça me va.
--------------
L'idée des surfaces de Bézier pour cette situation me semble la plus rapide, plutôt qu'un bidouillage analytique.
--------------
Je rappelle que j'ai bien compris comment fonctionne tout ça avec les quadrilatères,
mais qu'avec les triangles, c'est flou.
Dans l'exemple de GM, que sont ces points rouges exactement ? J'ai juste une vague idée.
Je n'ai pas trouvé de doc, sur cet artefact du triangle, et comment l'utiliser proprement.
Sinon, je ferais des quadrilatères.
---------------
Et des trajectoires dessinées en diagonale, c'est possible ?
(comme uequals et vequals qui donnent des "parallèles")
Merci pour toutes vos infos.
Il y a un théorème qui dit vaguement qu'une surface convexe, compacte, et avec des trous
peut être vue comme une associations de pantalon.
Il s'intéresse aux classes d'équivalences.
Un tore à deux trous, est dans la classe de deux pantalons raboutés par le tronc.
Les pattes de chaque pantalon se soudent face à face.
Ainsi peu importe la définition analytique à partir du moment où un bretzel a bien 3 trous ...
--------------
Il souhaite dessiner de nombreux pantalons, et je vais essayer de lui proposer un programme python (ou autre)
qui crache le bon code asymptote.
Il me faut une fonction pantalon à 6 paramètres.
3 points de sortie, et trois vecteurs "débit" associés.
Et oui, les manchons ne sont pas forcément parallèles.
Plus le débit est gros, plus le "disque" sera large. Le débit est normal à ce disque.
--------------
Je dit "disque" car, si j'ai bien compris, les surfaces de Bézier ne fournissent qu'une "très bonne" approximation du disque.
Et ça me va.
--------------
L'idée des surfaces de Bézier pour cette situation me semble la plus rapide, plutôt qu'un bidouillage analytique.
--------------
Je rappelle que j'ai bien compris comment fonctionne tout ça avec les quadrilatères,
mais qu'avec les triangles, c'est flou.
Dans l'exemple de GM, que sont ces points rouges exactement ? J'ai juste une vague idée.
Je n'ai pas trouvé de doc, sur cet artefact du triangle, et comment l'utiliser proprement.
Sinon, je ferais des quadrilatères.
---------------
Et des trajectoires dessinées en diagonale, c'est possible ?
(comme uequals et vequals qui donnent des "parallèles")
Merci pour toutes vos infos.
Re: Comment tailler un short ?
Francky a écrit :
Je rappelle que j'ai bien compris comment fonctionne tout ça avec les quadrilatères,
mais qu'avec les triangles, c'est flou.
Dans l'exemple de GM, que sont ces points rouges exactement ? J'ai juste une vague idée.
Je n'ai pas trouvé de doc, sur cet artefact du triangle, et comment l'utiliser proprement.
Sinon, je ferais des quadrilatères.
---------------
Et des trajectoires dessinées en diagonale, c'est possible ?
(comme uequals et vequals qui donnent des "parallèles")
Merci pour toutes vos infos.
1) relire les messages (triangle est un artifice ici),
lire les codes sources de three_surface.asy, trouver des
infos sur les surfaces de Bézier et tester. Je n'en sais pas
plus.
2) relire la fin de mon dernier message et tester le code avec
octants.point(i/10,i/10)
Pour tes shorts/pantalons la difficulté sera le recollement
des trois morceaux. Mais d'après ce que je comprends tu ne
demandes pas nécessairemement d'avoir une surface lisse,
cela facilite le recollement de 3 cylindres.
bon courage
O.G.

