merging two cylinders and make the base flat in Asymptote
Règles du forum
Pour toute demande d'aide pour la conception (ou la confirmation d'un code) d'une figure Asymptote, c'est ici.
J'invite ceux qui ont régulièrement des questions à poser à aller dans leur panneau de l'utilisateur pour indiquer dans la signature de leurs messages :
On va gagner du temps dans les réponses !
Pour toute demande d'aide pour la conception (ou la confirmation d'un code) d'une figure Asymptote, c'est ici.
J'invite ceux qui ont régulièrement des questions à poser à aller dans leur panneau de l'utilisateur pour indiquer dans la signature de leurs messages :
- Nom du système d'exploitation (W7 ou Ubuntu 12.04 ou ...)
- Version d'Asymptote et éditeur utilisé pour les figures Asymptote
- Distribution LaTeX et éditeur utilisé pour les tex.
On va gagner du temps dans les réponses !
merging two cylinders and make the base flat in Asymptote
Hi I am new to the Asymptote. I actually wanted to recreate the following figure using asymptote. I don't know how to merge two cylinders and make the bottom surface flat.
Name of OS: win10
Asymptote 2.41 version
Name of OS: win10
Asymptote 2.41 version
Re: merging two cylinders and make the base flat in Asymptote
Hello,
It's a figure that's difficult to create.
With the following code, the figure obtained seems to approach what is requested but by changing certain values of the parameters, it can be seen that the code needs to be improved.
Sorry not to be able to offer better.
It's a figure that's difficult to create.
With the following code, the figure obtained seems to approach what is requested but by changing certain values of the parameters, it can be seen that the code needs to be improved.
Sorry not to be able to offer better.
- crop3D.asy (file from Charles Staats to put in directory .asy)
Code : Tout sélectionner
import three; /**********************************************/ /* Code for splitting surfaces: */ struct possibleInt { int value; bool holds; } // Get versions of hsplit and vsplit with no extra optional // argument. triple[][][] old_hsplit(triple[][] P) { return hsplit(P); } triple[][][] old_vsplit(triple[][] P) { return vsplit(P); } int operator cast(possibleInt i) { return i.value; } restricted int maxdepth = 20; restricted void maxdepth(int n) { maxdepth = n; } surface[] divide(surface s, possibleInt region(patch), int numregions, bool keepregion(int) = null) { if (keepregion == null) keepregion = new bool(int region) { return (0 <= region && region < numregions); }; surface[] toreturn = new surface[numregions]; for (int i = 0; i < numregions; ++i) toreturn[i] = new surface; void addPatch(patch P, int region) { if (keepregion(region)) toreturn[region].push(P); } void divide(patch P, int depth) { if (depth == 0) { addPatch(P, region(P)); return; } possibleInt region = region(P); if (region.holds) { addPatch(P, region); return; } // Choose the splitting function based on the parity of the recursion depth. triple[][][] Split(triple[][] P) = (depth % 2 == 0 ? old_hsplit : old_vsplit); patch[] Split(patch P) { triple[][][] patches = Split(P.P); return sequence(new patch(int i) {return patch(patches[i]);}, patches.length); } patch[] patches = Split(P); for (patch PP : patches) divide(PP, depth-1); } for (patch P : s.s) divide(P, maxdepth); return toreturn; } surface[] divide(surface s, int region(triple), int numregions, bool keepregion(int) = null) { possibleInt patchregion(patch P) { triple[][] controlpoints = P.P; possibleInt theRegion; theRegion.value = region(controlpoints[0][0]); theRegion.holds = true; for (triple[] ta : controlpoints) { for (triple t : ta) { if (region(t) != theRegion.value) { theRegion.holds = false; break; } } if (!theRegion.holds) break; } return theRegion; } return divide(s, patchregion, numregions, keepregion); } /**************************************************/ /* Code for cropping surfaces */ // Return 0 iff the point lies in box(a,b). int cropregion(triple pt, triple a=O, triple b=(1,1,1)) { real x=pt.x, y=pt.y, z=pt.z; int toreturn=0; real xmin=a.x, xmax=b.x, ymin = a.y, ymax=b.y, zmin=a.z, zmax=b.z; if (xmin > xmax) { xmin = b.x; xmax = a.x; } if (ymin > ymax) { ymin = b.y; ymax = a.y; } if (zmin > zmax) { zmin = b.z; zmax = a.z; } if (x < xmin) --toreturn; else if (x > xmax) ++toreturn; toreturn *= 2; if (y < ymin) --toreturn; else if (y > ymax) ++toreturn; toreturn *= 2; if (z < zmin) --toreturn; else if (z > zmax) ++toreturn; return toreturn; } // Crop the surface to box(a,b). surface crop(surface s, triple a, triple b) { int region(triple pt) { return cropregion(pt, a, b); } return divide(s, region=region, numregions=1)[0]; } // Crop the surface to things contained in a region described by a bool(triple) function surface crop(surface s, bool allow(triple)) { int region(triple pt) { if (allow(pt)) return 0; else return -1; } return divide(s, region=region, numregions=1)[0]; } /******************************************/ /* Code for cropping paths */ // A rectangular solid with opposite vertices a, b: surface surfacebox(triple a, triple b) { return shift(a)*scale((b-a).x,(b-a).y,(b-a).z)*unitcube; } bool containedInBox(triple pt, triple a, triple b) { return cropregion(pt, a, b) == 0; } // Crop a path3 to box(a,b). path3[] crop(path3 g, triple a, triple b) { surface thebox = surfacebox(a,b); path3[] toreturn; real[] times = new real[] {0}; real[][] alltimes = intersections(g, thebox); for (real[] threetimes : alltimes) times.push(threetimes[0]); times.push(length(g)); for (int i = 1; i < times.length; ++i) { real mintime = times[i-1]; real maxtime = times[i]; triple midpoint = point(g, (mintime+maxtime)/2); if (containedInBox(midpoint, a, b)) toreturn.push(subpath(g, mintime, maxtime)); } return toreturn; } path3[] crop(path3[] g, triple a, triple b) { path3[] toreturn; for (path3 gi : g) toreturn.append(crop(gi, a, b)); return toreturn; } /***************************************/ /* Code to return only the portion of the surface facing the camera */ bool facingCamera(triple vec, triple pt=O, projection P = currentprojection, bool towardsCamera = true) { triple normal = P.camera; if (!P.infinity) { normal = P.camera - pt; } if (towardsCamera) return (dot(vec, normal) >= 0); else return (dot(vec, normal) <= 0); } surface facingCamera(surface s, bool towardsCamera = true, int maxdepth = 10) { int oldmaxdepth = maxdepth; maxdepth(maxdepth); possibleInt facingregion(patch P) { int n = 2; possibleInt toreturn; unravel toreturn; bool facingcamera = facingCamera(P.normal(1/2, 1/2), pt=P.point(1/2,1/2), towardsCamera); value = facingcamera ? 0 : 1; holds = true; for (int i = 0; i <= n; ++i) { real u = i/n; for (int j = 0; j <= n; ++j) { real v = j/n; if (facingCamera(P.normal(u,v), P.point(u,v), towardsCamera) != facingcamera) { holds = false; break; } } if (!holds) break; } return toreturn; } surface toreturn = divide(s, facingregion, numregions=1)[0]; maxdepth(oldmaxdepth); return toreturn; } - FIGURE
Code : Tout sélectionner
import solids; import crop3D; import math; size(8cm,0); currentprojection=orthographic(4,2,-1,up=Z); currentlight=White; path3 xyplan = path3(scale(2) * box((-1,-1),(1,1))); real a=2, thetai=45, thetar=50; triple A=(0,-a*sin(thetai*pi/180),a*cos(thetai*pi/180)), Ap=-A, // A--Ap axe Cylindre 1 B=(0,a*sin(thetar*pi/180),a*cos(thetar*pi/180)), Bp=-B; // B--Bp axe Cylindre 2 dot("A",A); dot("A'",Ap); dot("B",B); dot("B'",Bp); real ray=1, long1=abs(Ap-A), long2=abs(Bp-B); surface cyl1 = surface( rotate(thetai,X) * shift((0,0,-long1/2)) * cylinder(O,ray,long1) ), cyl2 = surface( rotate(-thetar,X) * shift((0,0,-long2/2)) * cylinder(O,ray,long2) ); bool Condition1 (triple ppt) { return (ppt.z>=0)&&(abs(ppt-point(B--Bp,intersect(B,Bp,Bp-B,ppt)))-ray>0); } bool Condition2 (triple ppt) { return (ppt.z>=0)&&(abs(ppt-point(A--Ap,intersect(A,Ap,Ap-A,ppt)))-ray>0); } surface cropcyl1 = crop(cyl1, Condition1); surface cropcyl2 = crop(cyl2, Condition2); draw(surface(xyplan),black+opacity(.5)); draw(xyplan,black+linewidth(.1)); draw(cropcyl1,red); draw(cropcyl2,blue);
Index des fonctions - Exemple de lien donnant le résultat d'une recherche sur les mots 'arc' et 'triple' : http://asy.marris.fr/indexasy/?filtre=arc triple
Mes configurations (le 24/02/21) :
PC n°1 :Windows 10 - Asymptote(2.82)+MikTeX2.9 - Editeurs : Notepad++, TeXworks, Visual Studio Code.
PC n°2 : Ubuntu 20.04LTS - Asymptote(2.67-?? git) + TexLive2020
Mon serveur : Debian Stretch- Asymptote(2.68-16 git) + TexLive2018
Merci de préciser la votre !
Mes configurations (le 24/02/21) :
PC n°1 :Windows 10 - Asymptote(2.82)+MikTeX2.9 - Editeurs : Notepad++, TeXworks, Visual Studio Code.
PC n°2 : Ubuntu 20.04LTS - Asymptote(2.67-?? git) + TexLive2020
Mon serveur : Debian Stretch- Asymptote(2.68-16 git) + TexLive2018
Merci de préciser la votre !
Re: merging two cylinders and make the base flat in Asymptote
Probably the author of the file "crop3D.asy" will be more able to propose a good way to create this figure :
http://math.uchicago.edu/~cstaats/
http://math.uchicago.edu/~cstaats/
Index des fonctions - Exemple de lien donnant le résultat d'une recherche sur les mots 'arc' et 'triple' : http://asy.marris.fr/indexasy/?filtre=arc triple
Mes configurations (le 24/02/21) :
PC n°1 :Windows 10 - Asymptote(2.82)+MikTeX2.9 - Editeurs : Notepad++, TeXworks, Visual Studio Code.
PC n°2 : Ubuntu 20.04LTS - Asymptote(2.67-?? git) + TexLive2020
Mon serveur : Debian Stretch- Asymptote(2.68-16 git) + TexLive2018
Merci de préciser la votre !
Mes configurations (le 24/02/21) :
PC n°1 :Windows 10 - Asymptote(2.82)+MikTeX2.9 - Editeurs : Notepad++, TeXworks, Visual Studio Code.
PC n°2 : Ubuntu 20.04LTS - Asymptote(2.67-?? git) + TexLive2020
Mon serveur : Debian Stretch- Asymptote(2.68-16 git) + TexLive2018
Merci de préciser la votre !
Re: merging two cylinders and make the base flat in Asymptote
Thank you GM, Since I am very new to Asymptote, there is a doubt in few keywords. I searched for the keyword "patch", but I couldn't able to find proper definition. I will take some time to understand the code that you have replied
Re: merging two cylinders and make the base flat in Asymptote
===========
I'm not a beginner in the use of Asymptote but I confess to have used it, almost exclusively, for the 2D geometry.
I hope, for many years, that Asymptote will be improved for 3D geometry (intersections, dashed hidden lines, resolution of the problem of insufficient memory, ...) but I suppose that they're not easy problems to solve for the authors of Asymptote.
It is courageous to study the crop3D.asy file but I admit to having used it without studying it: I discovered the existence of this file yesterday.
===========
Je ne suis pas un débutant dans l'utilisation d'Asymptote mais j'avoue l'avoir utilisé, quasiment exclusivement, pour la géométrie 2D.
J'espère, depuis de nombreuses années, qu'Asymptote sera amélioré pour la géométrie 3D (intersections, traits cachés en pointillés, résolution du problème de mémoire insuffisante, ...) mais je suppose que ce ne sont pas des problèmes faciles à résoudre pour les auteurs d'Asymptote.
C'est courageux d'étudier le fichier crop3D.asy mais j'avoue l'avoir utilisé sans l'étudier: j'ai découvert l'existence de ce fichier hier.
===========
For an example of a patch, i can't propose a better rendering on the forum with "settings.render = 0". Try again on your own pc without "settings.render = 0".
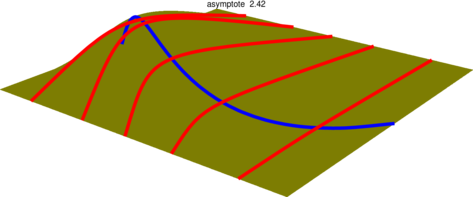
*** Pour masquer/découvrir le code Asymptote qui a permis de créer la figure, il faut cliquer dessus. ;-) ***
- CODE ASYMPTOTE de la figure ci-dessus : Tout sélectionner
- settings.render=0;
- import three;
- size(10cm);
- currentlight=White;
- surface s=surface(patch(new triple[][] {
- {(0,0,0),(1,0,0),(1,0,0),(2,0,0)},
- {(0,1,0),(1,0,1),(1,0,1),(2,1,0)},
- {(0,1,0),(1,0,-1),(1,0,-1),(2,1,0)},
- {(0,2,0),(1,2,0),(1,2,0),(2,2,0)}}));
- draw(s,yellow);
- draw(s.s[0].vequals(0.5),squarecap+2bp+blue,currentlight);
- draw(s.s[0].uequals(0.1),squarecap+2bp+red,currentlight);
- draw(s.s[0].uequals(0.3),squarecap+2bp+red,currentlight);
- draw(s.s[0].uequals(0.5),squarecap+2bp+red,currentlight);
- draw(s.s[0].uequals(0.7),squarecap+2bp+red,currentlight);
- draw(s.s[0].uequals(0.9),squarecap+2bp+red,currentlight);
Index des fonctions - Exemple de lien donnant le résultat d'une recherche sur les mots 'arc' et 'triple' : http://asy.marris.fr/indexasy/?filtre=arc triple
Mes configurations (le 24/02/21) :
PC n°1 :Windows 10 - Asymptote(2.82)+MikTeX2.9 - Editeurs : Notepad++, TeXworks, Visual Studio Code.
PC n°2 : Ubuntu 20.04LTS - Asymptote(2.67-?? git) + TexLive2020
Mon serveur : Debian Stretch- Asymptote(2.68-16 git) + TexLive2018
Merci de préciser la votre !
Mes configurations (le 24/02/21) :
PC n°1 :Windows 10 - Asymptote(2.82)+MikTeX2.9 - Editeurs : Notepad++, TeXworks, Visual Studio Code.
PC n°2 : Ubuntu 20.04LTS - Asymptote(2.67-?? git) + TexLive2020
Mon serveur : Debian Stretch- Asymptote(2.68-16 git) + TexLive2018
Merci de préciser la votre !
