import fontsize;
//usepackage("fourier");
picture tabsgn(string[][] tab, real ul=1, real kx=1.1, real ky=1.2 ,pen p=1bp+black, bool m=true){
picture pic;
string d=(m==true)?"$":"";
pen stylo=fontsize(ul*10pt);
int n=tab.length;
object[] obj=new object[tab.length];
real larg,haut;
for(int k=0; k<n; ++k){
obj[k]=object(Label("$"+tab[k][0]+"$",stylo));
larg=max(larg,(max(obj[k])-min(obj[k])).x);
haut=max(haut,(max(obj[k])-min(obj[k])).y);
}
string[] lx;
lx=split(tab[0][1]," ");
object[] lxo=new object[lx.length];
real xlarg,xhaut,dxl=1.1;
for(int k=0; k<lx.length; ++k){
lxo[k]=object(Label(d+((m==true)?replace(lx[k],"inf","\infty"):lx[k])+d,stylo));
xlarg=max(xlarg,(max(lxo[k])-min(lxo[k])).x);
}
larg*=kx/2; haut*=ky/2; xlarg*=kx*1.5;
draw(pic,(-larg,haut-2n*haut)--(-larg,haut)--(larg,haut)--(larg,haut-2n*haut),p);
for(int k=0; k<n; ++k){
add(pic,shift(0,-2k*haut)*obj[k]);
draw(pic,(-larg,haut-2(k+1)*haut)--(larg,haut-2(k+1)*haut),p);
real L=(lxo.length-1/2)*xlarg;
if(k==0) {
draw(pic,(larg,haut)--(dxl^2*larg+L,haut)--(dxl^2*larg+L,-haut)--(larg,-haut),p);
for(int kk=0; kk<lxo.length; ++kk)
add(pic,shift(dxl*larg+(1/4+kk)*xlarg,0)*lxo[kk]);
} else {
string[] ly;
real l=xlarg/30;
ly=split(tab[k][1]," ");
for(int j=0; j<ly.length; ++j){
real xla = dxl*larg+(1/4+j/2)*xlarg;
if(ly[j]=="O") {
draw(pic,circle((xla,-k*2haut),haut/2),linewidth(1bp));
draw(pic,(xla,-k*2haut-haut)--(xla,-k*2haut+haut),p); }
else if(ly[j]=="0") {
label(pic,shift(xla,-k*2haut)*(d+ly[j]+d),stylo);
draw(pic,(xla,-k*2haut-haut)--(xla,-k*2haut+haut),p); }
else if(ly[j]=="|")
draw(pic,(xla,-k*2haut-haut)--(xla,-k*2haut+haut),p);
else if(ly[j]=="||")
draw(pic,(xla-l,-k*2haut-haut)--(xla-l,-k*2haut+haut)
^^(xla+l,-k*2haut-haut)--(xla+l,-k*2haut+haut),linewidth(1bp));
else label(pic,shift(xla,-k*2haut)*(d+ly[j]+d),stylo);
}
draw(pic,(dxl^2*larg+L,haut-k*2haut)--(dxl^2*larg+L,-haut-k*2haut)--(larg,-haut-k*2haut),p);
}
}
return pic;
}
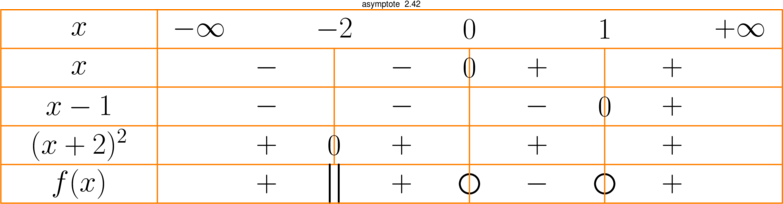
string[][] tab={
{"x", "-inf -2 0 1 +inf"},
{"x", " - | - 0 + | + "},
{"x-1", " - | - | - 0 + "},
{"(x+2)^2", " + 0 + | + | + "},
{"f(x)", " + || + O - O + "}
};
add(tabsgn(tab,ul=1.8,kx=1.5,ky=1,p=.8bp+orange)); // ul=1.1 pour 11pt, ul=1.2 pour 12pt